
����Ŀ��Ϊ�˹᳹��ʵ��ί���������������ƶ������ijУ���ƶ���һϵ�а��A��B��ƶ����ļƻ����־�����ij������152�����絽A��B������ֳ�����ô�С������15������ǡ����һ���������������磬��֪�����ִ�С�������ػ������ֱ�Ϊ12��/����8��/����������A��B������˷������
���� | Ŀ�ĵ� | |
A�壨Ԫ/���� | B�壨Ԫ/���� | |
����� | ||
800 | 900 | |
���� | 400 | 600 |
��1������15�����д�С��������������
��2���ְ�������10������ǰ��A�壬�������ǰ��B�壬��ǰ��A��Ĵ����Ϊx����ǰ��A��B�����ܷ���ΪyԪ�������y��x�ĺ�������ʽ��
��3���ڣ�2���������£�������A������粻����100�䣬����д��ʹ�ܷ������ٵĻ������䷽������������ٷ��ã�
���𰸡���1���������8����С������7������2��y=100x+9400����3��������.
��������
���⣨1����������x����С������y�������ݴ�С���ֻ�����15��������152�����磬�з�������⣻
��2����ǰ��A��Ĵ����Ϊx������ǰ��B��Ĵ����Ϊ��8-x������ǰ��A���С����Ϊ��10-x������ǰ��B���С����Ϊ[7-��10-x��]�������ݱ��������˷ѣ����y��x�ĺ�����ϵʽ��
��3�������֪��������x��ȡֵ��Χ���ɣ�2���ĺ�����ϵʽ��ʹ���˷����ٵĻ������䷽����
�����������1����������x����С������y������������ã�![]()
��ã�![]() �����������8����С������7����
�����������8����������7����
��2��y=800x+900��8-x��+400��10-x��+600[7-��10-x��]=100x+9400����3��x��8����x��������
��3��������ã�12x+8��10-x����100����ã�x��5������3��x��8����5��x��8��Ϊ������
��y=100x+9400��k=100��0��y��x���������������x=5ʱ��y��С��
��СֵΪy=100��5+9400=9900��Ԫ����
��ʹ���˷����ٵĵ��䷽���ǣ�5���������5��С����ǰ��A�壻3���������2��С����ǰ��B�壮�����˷�Ϊ9900Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��һ���������̣�����Ϸ������һ�����Ӵ�ijһ����ʼ�ǿ�ʼ���������ɲ������Ժ����յ������ʱ��ÿһ��ֻ����������ͬλ�ǻ��ڴ��ǻ�ͬ���ڽǵ�λ�������磺����ʼλ��![]() �����յ�λ��
�����յ�λ��![]() �����ֲ�ͬ·����·��1��
�����ֲ�ͬ·����·��1��![]() ��·��2��
��·��2��![]() .
.

��һ�ԣ���1��д������ʼλ��![]() �����յ�λ��
�����յ�λ��![]() ��һ��·����
��һ��·����
��2������ʼλ��![]() ���ΰ�ͬλ�ǡ��ڴ��ǡ�ͬ���ڽǵ�˳�������ܷ������յ�λ��
���ΰ�ͬλ�ǡ��ڴ��ǡ�ͬ���ڽǵ�˳�������ܷ������յ�λ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���ڸ����Ķ��κ���y=a��x��h��2+k��a��0���������һ�κ���Ϊy=a��x��h��+k�����磺���κ���y=2��x+1��2��3�İ���һ�κ���Ϊy=2��x+1����3����y=2x��1��
��1����֪���κ���y=��x��1��2��4���������һ�κ����ı���ʽΪ_____��
��2����˵�����κ���y=��x��1��2��4�Ķ����������һ�κ�����ͼ���ϣ�
��3����ͼ�����κ���y=m��x��1��2��4m��m��0���İ���һ�κ�����ͼ����x�ᡢy��ֱ��ڵ�B��A����������ͼ��Ľ���ĺ�����ֱ�Ϊ1��2���ڡ�AOB�ڲ��Ķ��κ���y=m��x��1��2��4m��ͼ������һ����P������P��x���ƽ�����������һ�κ�����ͼ���ڵ�Q�����P�ĺ�����Ϊn��ֱ��д���߶�PQ�ij�Ϊ![]() ʱn��ֵ��
ʱn��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ��������ũ�壬��ί������������εؿ�ͳ����εؿ����Ͻ����̻�.�����ؿ��ڷֱ���һ���߳�Ϊa�Ĵ������λ�̳���ĸ��߳�Ϊb��С�����λ�̳(��Ӱ����)���հ����������ƺ����S1��ʾ�ؿ���пհ״������ƺ�������S2��ʾ�ؿ����пհ״������ƺ�������
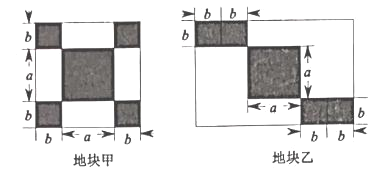
��1��S1=________��S2=________(�ú�a��b�Ĵ���ʽ��ʾ������) .
��2����a=2b�����![]() ֵ
ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
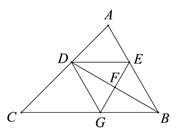
����Ŀ����ͼ��BD�ǡ�ABC�Ľ�ƽ���ߣ����Ĵ�ֱƽ���߷ֱ�AB��BD��BC�ڵ�E��F��G������DE��DG��
��1�����ж��ı���EBGD����״����˵�����ɣ�
��2������ABC=60������C=45����DE=![]() ����BC�ij���
����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ij��Ϳ��ֱ�Ϊ6��4��E��F��G��H�����Ǿ���ABCD���ߵ��е㣬���ı���EFGH���ܳ�����( )
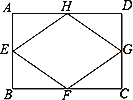
A. 20B. 10C. 4![]() D. 2
D. 2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O(0��0)��A(0��1)��������OAA1B���������㣬�ԶԽ���OA1Ϊ����������OA1A2B1�����������εĶԽ���OA2��������OA2A3B3���������˹��ɣ����A10��������_____��
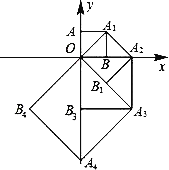
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017����ʡ�����У���������������˾������һ���ļ���װ��ͨ��ʵ���̵�������̵�����;���������ۣ�����һ��ʱ��ù�˾��������Ʒ�����������������Ϊ��30��ĸ��ٵ��飬����ʵ���̵����������y1���ټ�����ʱ��t��tΪ��������λ���죩�IJ��ֶ�Ӧֵ���±���ʾ�������̵����������y2���ټ�����ʱ��t��tΪ��������λ���죩�IJ��ֶ�Ӧֵ��ͼ��ʾ��
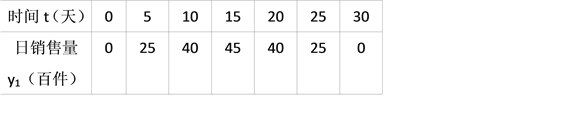
��1��������һ�κ��������κ����ͷ����������У�ѡ����ʵĺ����ܷ�ӳy1��t�ı仯���ɣ������y1��t�ĺ�����ϵʽ���Ա���t��ȡֵ��Χ��
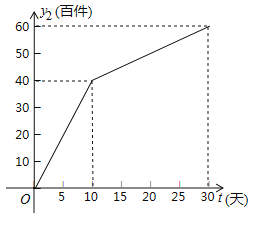
��2����y2��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
��3���ڸ��ٵ����30���У���ʵ���̵�������̵������������Ϊy���ټ�������y��t�ĺ�����ϵʽ����tΪ��ֵʱ������������y�ﵽ��������ʱ�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com