Question

【题目】如图，BD是△ABC的角平分线，它的垂直平分线分别交AB，BD，BC于点E，F，G，连接DE，DG．

（1）请判断四边形EBGD的形状，并说明理由；

（2）若∠ABC=60°，∠C=45°，DE=，求BC的长．

Answer 1

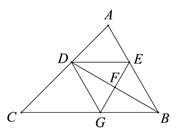
【答案】（1）四边形EBGD为菱形（2）3+3

【解析】试题分析：（1）先证明四边形BEDG为平行四边形，再根据一组邻边相等的平行四边形得出四边形EBGD为菱形．
（2）作EM⊥BC于M，先求得BM和CM的值，再根据BC＝BM+CM即可．

试题解析：

（1）四边形EBGD为菱形；

理由：∵EG垂直平分BD，

∴EB=ED，GB=GD，

∴∠EBD=∠EDB，

∵∠EBD=∠DBC，

∴∠EDF=∠GBF，

∴DE∥BG，同理BE∥DG，

∴四边形BEDG为平行四边形，

又∵DE=BE，

∴四边形EBGD为菱形；

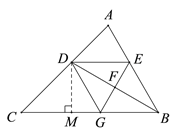
（2）如答图，过D作DM⊥BC于M，由（1）知，∠DGC=∠ABC=60°，∠DBM=∠ABC=30°，DE=DG=，

∴在Rt△DMG中，得DM=3，在Rt△DMB中，得BM=，

又∵∠C=45°，

∴CM=DM=3，

∴BC=3+．