
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y轴交于点C.
(1)点A的坐标为 ,点B的坐标为 ,点C的坐标为 .
(2)设抛物线y=x2﹣2x﹣3的顶点为M,求四边形ABMC的面积.
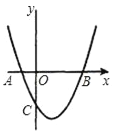
【答案】(1)A(﹣1,0),B(3,0),C(0,﹣3);(2)9.
【解析】
试题分析:(1)把y=0和x=0分别代入解析式即可求出A、B、C的坐标;
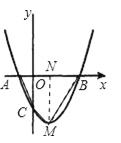
(2)把解析式化成顶点式即可求出M的坐标,过M作MN⊥X轴于N,这样四边形ACMB的面积就转化成△ACO、梯形OCMN、△BMN的面积,根据点的坐标求出各个面积代入即可.
试题解析:(1)当y=0时,x2﹣2x﹣3=0,解得:x1=3,x2=﹣1,∴点A的坐标是(﹣1,0),点B的坐标是(3,0),当x=0时,y=﹣3,∴点C的坐标是(0,﹣3),故答案为:A(﹣1,0),B(3,0),C(0,﹣3);
(2)解:y=x2﹣2x﹣3=(x﹣1)2﹣4,∴M(1,﹣4),过M作MN⊥X轴于N,则:ON=1,MN=4,BN=3﹣1=2,OA=1,OC=3,∴四边形ABMC的面积S=S△COA+S梯形CONM+S△BNM=![]() OA×OC+
OA×OC+![]() ×(OC+MN)×ON+
×(OC+MN)×ON+![]() ×MN×BN=
×MN×BN=![]() ×1×3+
×1×3+![]() ×(3+4)×1+
×(3+4)×1+![]() ×2×4=9.
×2×4=9.
答:四边形ABMC的面积是9.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲乙两同学用一副扑克牌中牌面数字分别是3,4,5,6的4张牌做抽数字游戏,游戏规则是:将这4张牌的正面全部朝下,洗匀,从中随机抽取一张,抽得的数作为十位上的数字,抽出的牌不放回,然后将剩下的牌洗匀,再从中随机抽取一张,抽得的数作为个位上的数字,这样就得到一个两位数,若这个两位数小于45,则甲获胜,否则乙获胜.你认为这个游戏公平吗?请利用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=2,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于2,则α=( )
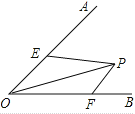
A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在∠POQ内部有两点M、N,∠MOP=∠NOQ.
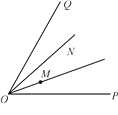
(1)画图并简要说明画法:在射线OP上取一点A,使点A到点M和点N的距离和最小;在射线OQ上取一点B,使点B到点M和点N的距离和最小;
(2)直接写出AM+AN与BM+BN的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com