
【题目】如图,已知在等腰三角形ABC中,AB=AC,P,Q分别是边AC,AB上的点,且AP=PQ=QC=BC.则∠PCQ的度数为________.

【答案】(![]() )°
)°
【解析】
根据等边对等角得出∠ABC=∠ACB,∠A=∠AQP,∠QPC=∠QCP,∠BQC=∠B,设∠A=x°,则∠AQP=x°,根据三角形的外角性质求出∠QPC=∠PCQ=2x°,∠BQC=3x°,∠ACB=∠B=3x°.在△ABC中根据三角形的内角和定理得出方程x°+3x°+3x°=180°,解方程求出即可.
∵AB=AC,AP=PQ,QP=QC,QC=BC,∴∠ABC=∠ACB,∠A=∠AQP,∠QPC=∠QCP,∠BQC=∠B(等边对等角),
设∠A=x°,则∠AQP=x°,
∵在△AQP中,∠QPB是外角,∴∠QPC=∠A+∠AQP=2x°(三角形的一个外角等于和它不相邻的两个内角的和),
∵在△BCQ中,∠BQC是外角,∴∠BQC=∠ACQ+∠A(三角形的一个外角等于和它不相邻的两个内角的和),∴∠BQC=3x°,∴∠B=3x°,∴∠ABC=3x°,
∵在△ABC中,∠A+∠ACB+∠B=180°,∴x°+3x°+3x°=180°(三角形三个内角的和等于180°),
解得:x=(![]() )°,∴∠PCQ=2x=(
)°,∴∠PCQ=2x=(![]() )°.
)°.
故答案为:(![]() )°.
)°.


科目:初中数学 来源: 题型:
【题目】阅读理解:
我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1)、Q(x2,y2)的对称中心的坐标为(![]() ,
,![]() ).
).
观察应用:
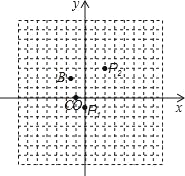
(1)如图,在平面直角坐标系中,若点P1(0,﹣1)、P2(2,3)的对称中心是点A,则点A的坐标为 ;
(2)另取两点B(﹣1.6,2.1)、C(﹣1,0).有一电子青蛙从点P1处开始依次关于点A、B、C作循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…则点P3、P8的坐标分别为 、 .
拓展延伸:
(3)求出点P2012的坐标,并直接写出在x轴上与点P2012、点C构成等腰三角形的点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,调查方式选择不合理的是![]()
![]()
A. 调查我国中小学生观看电影![]() 厉害了,我的国
厉害了,我的国![]() 情况,采用抽样调查的方式
情况,采用抽样调查的方式
B. 调查全市居民对“老年餐车进社区”活动的满意程度,采用抽样调查的方式
C. 调查“神州十一号”运载火箭发射前零部件质量状况,采用全面调查![]() 普查
普查![]() 的方式
的方式
D. 调查市场上一批LED节能灯的使用寿命,采用全面调查![]() 普查
普查![]() 的方式
的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC.
【1】求证:△ABE≌△CDA;
【2】若∠DAC=40°,求∠EAC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BI,CI分别平分∠ABC,∠ACB,过I点作DE∥BC,交AB于D,交AC于E,给出下列结论:①△DBI是等腰三角形;②△ACI是等腰三角形;③AI平分∠BAC;④△ADE周长等于AB+AC.其中正确的是( )

A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙D的直径,AD切⊙D于点A,EC=CB.则下列结论:①BA⊥DA; ②OC∥AE;③∠COE=2∠CAE;④OD⊥AC.一定正确的个数有( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论: ①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正确的个数有( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com