
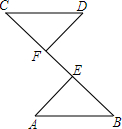
 如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )| A. | AE=DF | B. | ∠A=∠D | C. | ∠B=∠C | D. | AB=DC |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
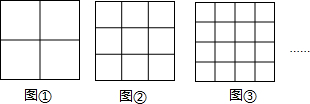
| A. | 72 | B. | 81 | C. | 100 | D. | 121 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
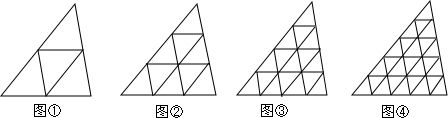
| 等分数n | 小三角形个数a | 顶点数b | 边数c |
| 2 | 4 | 6 | 9 |
| 3 | 9 | 10 | 18 |
| 4 | 16 | 15 | 30 |
| 5 | 25 | 21 | 45 |
| … | … | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示的圆柱体中底面圆的半径是$\frac{3}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是3$\sqrt{2}$(结果保留根号).
如图所示的圆柱体中底面圆的半径是$\frac{3}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是3$\sqrt{2}$(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com