练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】“端午”节前，第一次爸爸去超市购买了大小、质量都相同的火腿粽子和豆沙粽子若干，放入不透明的盒中，此时随机取出火腿粽子的概率为；妈妈发现小亮喜欢吃的火腿粽子偏少，第二次妈妈又去买了同样的5只火腿粽子和1只豆沙粽子放入同一盒中，这时随机取出火腿粽子的概率为．

    （1）请计算出第一次爸爸买的火腿粽子和豆沙粽子各有多少只？

    （2）若妈妈从盒中取出火腿粽子4只、豆沙粽子6只送爷爷和奶奶后，再让小亮从盒中不放回地任取2只，问恰有火腿粽子、豆沙粽子各1只的概率是多少？（用字母和数字表示豆沙粽子和火腿粽子，用列举法计算）

    【答案】（1）第一次爸爸买了4只火腿粽子，8只豆沙粽子．（2）恰好火腿粽子、豆沙粽子各1只的概率为．

    【解析】

    试题分析：（1）等量关系为：原来的火腿粽子数÷原来的总粽子数=；后来的火腿粽子数÷后来的总粽子数=；

    （2）列举出所有情况，看所求的情况占所有情况的概率如何．

    解：（1）设第一次爸爸买了x只火腿粽子，y只豆沙粽子．

    则：，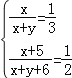

    解得：．

    经检验得出：x+y≠0，x+y+6≠0，

    ∴x=4，y=8是原方程的根，

    答：第一次爸爸买了4只火腿粽子，8只豆沙粽子．

    （2）现在有火腿粽子9只，豆沙粽子9只，送给爷爷，奶奶后，还有火腿粽子5只，豆沙粽子3只．

    记豆沙粽子a，b，c；火腿粽子1，2，3，4，5．恰好火腿粽子、豆沙粽子各1只的概率为=．

    第一次

    第二次

    a

    b

    c

    1

    2

    3

    4

    5

    a

    （a，b）

    （a，c）

    （a，1）

    （a，2）

    （a，3）

    （a，4）

    （a，5）

    b

    （b，a）

    （b，c）

    （b，1）

    （b，2）

    （b，3）

    （b，4）

    （b，5）

    c

    （c，a）

    （c，b）

    （c，1）

    （c，2）

    （c，3）

    （c，4）

    （c，5）

    1

    （1，a）

    （1，b）

    （1，c）

    （1，2）

    （1，3）

    （1，4）

    （1，5）

    2

    （2，a）

    （2，b）

    （2，c）

    （2，1）

    （2，3）

    （2，4）

    （2，5）

    3

    （3，a）

    （3，b）

    （3，c）

    （3，1）

    （3，2）

    （3，4）

    （3，5）

    4

    （4，a）

    （4，b）

    （4，c）

    （4，1）

    （4，2）

    （4，3）

    （4，5）

    5

    （5，a）

    （5，b）

    （5，c）

    （5，1）

    （5，2）

    （5，3）

    （5，4）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知长方形的面积为18x3y4+9xy2﹣27x2y2 ， 长为9xy，则宽为（ ）
    A.2x2y3+y+3xy
    B.2x2y2﹣2y+3xy
    C.2x2y3+2y﹣3xy
    D.2x2y3+y﹣3xy

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人从A,B两地出发，甲骑自行车，乙骑摩托车，沿同一条路线相向匀速行驶。出发后经3小时两人相遇。已知在相遇时乙比甲多行驶了90千米，相遇后经1小时乙达到A地。若设甲每小时行驶x千米，则可列方程为 _______________________ 。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：在正方形网格中有一个△ABC，按要求进行下列作图（只借助于网格，需写出结论）：

    （1）过点B画出AC的平行线；

    （2）画出先将△ABC向右平移5格，得到△A’B’C’，再向上平移3格后的△A”B”C”；

    （3）对于（2）里面这两次平移的得到的图形能通过△ABC一次性平移得到吗？如果可以请你用合适的语言描述这个过程。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果60米表示向东走60米，那么－40米表示_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】绝对值大于1且小于5的所有的整数的和是___________；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S1、S2 ， 则S1+S2的值为（　　）

    A. 16 B. 17 C. 18 D. 19

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB=AC，点D在边BC所在的直线上，过点D作DF∥AC交直线AB于点F，DE∥AB交直线AC于点E．

    （1）当点D在边BC上时，如图①，求证：DE+DF=AC．

    （2）当点D在边BC的延长线上时，如图②；当点D在边BC的反向延长线上时，如图③，请分别写出图②、图③中DE，DF，AC之间的数量关系，不需要证明．

    （3）若AC=6，DE=4，则DF= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有四张正面分别标有﹣1，0，1，2的不透明卡片，它们除数字不同外其余全部相同，现将它们背面朝上，洗匀后从中取出一张，将卡片上的数字记为a，不放回，再取出一张，将卡片上的数字记为b，设P点的坐标为（a，b）．如图，点P落在抛物线y=x2与直线y=x+2所围成的封闭区域内（图中含边界的阴影部分）的概率是 ．

    查看答案和解析>>

    同步练习册答案