
如图,直角三角形ABO放置在平面直角坐标系中,已知斜边OA在x轴正半轴上,且OA=4,AB=2,将该三角形绕着点O逆时针旋转120°后点B的对应点恰好落在一反比例函数图像上,则该反比例函数的解析式为 .
 .
.
解析试题分析:在Rt△ABO中,根据勾股定理计算出OB=2 ,利用正弦的定义得sin∠BOA=
,利用正弦的定义得sin∠BOA= ,则∠BOA=30°,设该三角形绕着点O逆时针旋转120°后点B的对应点为B′,根据旋转的性质得∠BOB′=120°,则OB′与x轴的负半轴的夹角为30°,且OB′=OB=2
,则∠BOA=30°,设该三角形绕着点O逆时针旋转120°后点B的对应点为B′,根据旋转的性质得∠BOB′=120°,则OB′与x轴的负半轴的夹角为30°,且OB′=OB=2 ,作B′H⊥x轴,在Rt△OB′H中,根据含30度的直角三角形三边的关系得B′H=
,作B′H⊥x轴,在Rt△OB′H中,根据含30度的直角三角形三边的关系得B′H= OB′=
OB′= ,OH=
,OH= B′H=3,所以B′点的坐标为(-3,
B′H=3,所以B′点的坐标为(-3, ),设点B′所落在的反比例函数解析式为y=
),设点B′所落在的反比例函数解析式为y= ,利用反比例函数图象上点的坐标特征得到k-3
,利用反比例函数图象上点的坐标特征得到k-3 ,从而得到该反比例函数的解析式为
,从而得到该反比例函数的解析式为 .
.
在Rt△ABO中,OA=4,AB=2,
∴OB= ,
,
sin∠BOA= ,
,
∴∠BOA=30°,
设该三角形绕着点O逆时针旋转120°后点B的对应点为B′,
∴OB′与x轴的负半轴的夹角为30°,OB′=OB=2 ,
,
作B′H⊥x轴,
在Rt△OB′H中,B′H= OB′=
OB′= ,OH=
,OH= B′H=3,
B′H=3,
∴B′点的坐标为(-3, ),
),
设点B′所落在的反比例函数解析式为 ,
,
∴k=-3× =-3
=-3
∴该反比例函数的解析式为 .
.
考点: 1.坐标与图形变化-旋转;2.反比例函数图象上点的坐标特征.


科目:初中数学 来源: 题型:填空题
已知点A(1,y1)、B(2,y2)、C(﹣3,y3)都在反比例函数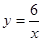 的图象上,则y1、y2、y3的大小关系是____________________.
的图象上,则y1、y2、y3的大小关系是____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°,如果点A在反比例函数y=(x>0)的图象上运动,那么点B在 (填函数解析式)的图象上运动.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)都在函数 (x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),已知点A1的坐标为(2,0),则点P1的坐标为 ;点P2的坐标为 ;点Pn的坐标为 (用含n的式子表示).
(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),已知点A1的坐标为(2,0),则点P1的坐标为 ;点P2的坐标为 ;点Pn的坐标为 (用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,M为双曲线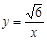 上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴、x轴分别交于点A、B,则AD•BC的值为 ;
上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴、x轴分别交于点A、B,则AD•BC的值为 ;
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图所示,点A、B在反比例函数 (k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,△AOC的面积为6,则k的值为 .
(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,△AOC的面积为6,则k的值为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com