
【题目】如图,直线l1的函数解析式为y=﹣2x+4,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.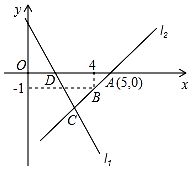
(1)求直线l2的函数解析式;
(2)求△ADC的面积;
(3)在直线l2上是否存在点P,使得△ADP面积是△ADC面积的2倍?如果存在,请求出P坐标;如果不存在,请说明理由.
【答案】
(1)解:设直线l2的函数解析式为y=kx+b,
将A(5,0)、B(4,﹣1)代入y=kx+b,
![]() ,解得:
,解得: ![]() ,
,
∴直线l2的函数解析式为y=x﹣5
(2)解:联立两直线解析式成方程组,
![]() ,解得:
,解得: ![]() ,
,
∴点C的坐标为(3,﹣2).
当y=﹣2x+4=0时,x=2,
∴点D的坐标为(2,0).
∴S△ADC= ![]() AD|yC|=
AD|yC|= ![]() ×(5﹣2)×2=3
×(5﹣2)×2=3
(3)解:假设存在.
∵△ADP面积是△ADC面积的2倍,
∴|yP|=2|yC|=4,
当y=x﹣5=﹣4时,x=1,
此时点P的坐标为(1,﹣4);
当y=x﹣5=4时,x=9,
此时点P的坐标为(9,4).,只需
综上所述:在直线l2上存在点P(1,﹣4)或(9,4),使得△ADP面积是△ADC面积的2倍.
【解析】第1小题,所求直线经过A、B两点,把y=kx+b这两点的坐标代入可求解;第2小题,要求三角形ADC的面积,只需求出C、D两点的坐标,点C是已知两直线的交点,联立解方程组可得坐标,点D是直线y=﹣2x+4与x轴的交点,问题的解;第3小题,这是一个存在性问题,假定存在,根据△ADP面积是△ADC面积的2倍计算,有解即存在,否则不存在。


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△ADE都是等边三角形.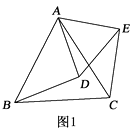
(1)求证:BD=CE;
(2)如图2,若BD的中点为P , CE的中点为Q , 请判断△APQ的形状,并说明理由.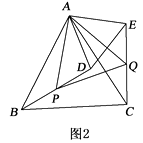
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且 ![]() =8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
=8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
(1)乙运动员射击训练成绩的众数是 , 中位数是 .
(2)求甲运动员射击成绩的平均数,并判断甲、乙两人在本次射击成绩的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)设计费能达到24000元吗?为什么?
(3)当x是多少米时,设计费最多?最多是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中,不能判定两直角三角形全等的是( )
A. 斜边和一锐角对应相等
B. 斜边上的中线和一直角边对应相等
C. 两边分别相等
D. 直角的平分线和一直角边对应相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com