
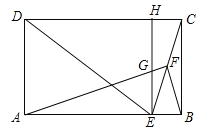
【题目】如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点.
(1)求证:DE=DC;
(2)求证:AF⊥BF;
(3)当AFGF=28时,请直接写出CE的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题(1)根据平行线的性质以及角平分线的定义,即可得到∠DCE=∠DEC,进而得出DE=DC;
(2)连接DF,根据等腰三角形的性质得出∠DFC=90°,再根据直角三角形斜边上中线的性质得出BF=CF=EF=![]() EC,再根据SAS判定△ABF≌△DCF,即可得出∠AFB=∠DFC=90°,据此可得AF⊥BF;
EC,再根据SAS判定△ABF≌△DCF,即可得出∠AFB=∠DFC=90°,据此可得AF⊥BF;
(3)根据等角的余角相等可得∠BAF=∠FEH,再根据公共角∠EFG=∠AFE,即可判定△EFG∽△AFE,进而得出EF2=AFGF=28,求得EF=![]() ,即可得到CE=2EF=
,即可得到CE=2EF=![]() .
.
试题解析:解:(1)∵四边形ABCD是矩形,∴AB∥CD,∴∠DCE=∠CEB,∵EC平分∠DEB,∴∠DEC=∠CEB,∴∠DCE=∠DEC,∴DE=DC;
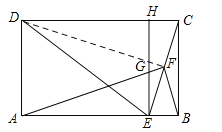
(2)如图,连接DF,∵DE=DC,F为CE的中点,∴DF⊥EC,∴∠DFC=90°,在矩形ABCD中,AB=DC,∠ABC=90°,∴BF=CF=EF=![]() EC,∴∠ABF=∠CEB,∵∠DCE=∠CEB,∴∠ABF=∠DCF,在△ABF和△DCF中,∵BF=CF,∠ABF=∠DCF,AB=DC,∴△ABF≌△DCF(SAS),∴∠AFB=∠DFC=90°,∴AF⊥BF;
EC,∴∠ABF=∠CEB,∵∠DCE=∠CEB,∴∠ABF=∠DCF,在△ABF和△DCF中,∵BF=CF,∠ABF=∠DCF,AB=DC,∴△ABF≌△DCF(SAS),∴∠AFB=∠DFC=90°,∴AF⊥BF;
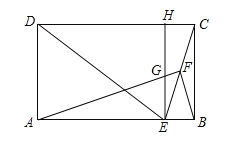
(3)CE=![]() .理由如下:∵AF⊥BF,∴∠BAF+∠ABF=90°,∵EH∥BC,∠ABC=90°,∴∠BEH=90°,∴∠FEH+∠CEB=90°,∵∠ABF=∠CEB,∴∠BAF=∠FEH,∵∠EFG=∠AFE,∴△EFG∽△AFE,∴
.理由如下:∵AF⊥BF,∴∠BAF+∠ABF=90°,∵EH∥BC,∠ABC=90°,∴∠BEH=90°,∴∠FEH+∠CEB=90°,∵∠ABF=∠CEB,∴∠BAF=∠FEH,∵∠EFG=∠AFE,∴△EFG∽△AFE,∴![]() ,即EF2=AFGF,∵AFGF=28,∴EF=
,即EF2=AFGF,∵AFGF=28,∴EF=![]() ,∴CE=2EF=
,∴CE=2EF=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
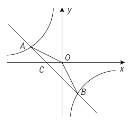
【题目】已知A(-4,2)、B(n,-4)两点是一次函数y=kx+b和反比例函数![]() 图象的两个交点.
图象的两个交点.
(1)求一次函数和反比例函数的解析式.
(2)求![]() 的面积.
的面积.
(3)观察图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
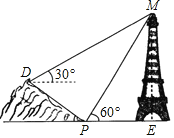
【题目】小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为![]() ,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为
,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为![]() .已知山坡坡度
.已知山坡坡度![]() ,即
,即![]() ,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据:
,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
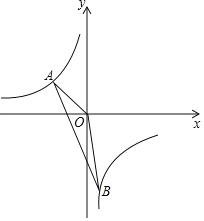
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A、B两点,点A的坐标是(﹣2,1),点B的坐标是(1,n);
的图象交于A、B两点,点A的坐标是(﹣2,1),点B的坐标是(1,n);
(1)分别求一次函数与反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式kx+b≥![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣4![]() x+12+m=0.
x+12+m=0.
(1)若方程的一个根是![]() ,求m的值及方程的另一根;
,求m的值及方程的另一根;
(2)若方程的两根恰为等腰三角形的两腰,而这个三角形的底边为m,求m的值及这个等腰三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM上的点,且MB=MN.

(1)求证:BN平分∠ABE;
(2)若BD=1,连结DN,当四边形DNBC为平行四边形时,求线段BC的长;
(3)如图②,若点F为AB的中点,连结FN、FM,求证:△MFN∽△BDC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com