练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

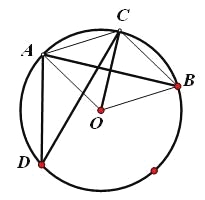
    【题目】如图，点A、B、C、D都在⊙O上，OC⊥AB，∠ADC＝30°.

    （1）求∠BOC的度数；

    （2）求证：四边形AOBC是菱形.

    【答案】（1）∠BOC的度数为60°；（2）证明见解析.

    【解析】

    （1）根据垂径定理得出，再利用圆周角定理得出∠BOC的度数；

    （2）根据等边三角形的判定得出BC=BO=CO，进而利用（1）中结论得出AO=BO=AC=BC，即可证明结论．

    (1)∵点A、B、C、D都在⊙O上，OC⊥AB，

    ∴，

    ∵∠ADC=30°，

    ∴∠AOC=∠BOC=2∠ADC=60°，

    ∴∠BOC的度数为60°；

    （2）证明：∵，

    ∴AC=BC，

    AO=BO，

    ∵∠BOC的度数为60°，BO=CO

    ∴△BOC为等边三角形，

    ∴BC=BO=CO，

    ∴AO=BO=AC=BC，

    ∴四边形AOBC是菱形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

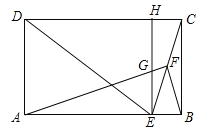
    【题目】如图，在矩形ABCD中，E为AB边上一点，EC平分∠DEB，F为CE的中点，连接AF，BF，过点E作EH∥BC分别交AF，CD于G，H两点．

    （1）求证：DE=DC；

    （2）求证：AF⊥BF；

    （3）当AFGF=28时，请直接写出CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

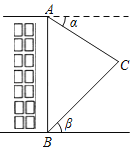
    【题目】如图，建筑物AB的高为52米，在其正前方广场上有人进行航模试飞.从建筑物顶端A处测得航模C的俯角α＝30°，同一时刻从建筑物的底端B处测得航模C的仰角β＝45°，求此时航模C的飞行高度.(精确到1米)(参考数据：≈1.41，≈1.73，≈2.45)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】、两组卡片共张，中三张分别写有数字，，，中两张分别写有，．它们除了数字外没有任何区别．

    随机地从中抽取一张，求抽到数字为的概率；

    随机地分别从、中各抽取一张，请你用画树状图或列表的方法表示所有等可能的结果，现制定这样一个游戏规则：若选出的两数之积为的倍数，则甲获胜；否则乙获胜．请问这样的游戏规则对甲乙双方公平吗？为什么？

    如果不公平请你修改游戏规则使游戏规则对甲乙双方公平．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两个同学做了一个数字游戏:拿出三张正面写有数字，2，3且背面完全相同的卡片，将这三张卡片背面朝上洗匀后，甲先随机抽取一张，将所得数字作为的值，然后将卡片放回并洗匀，乙再从这三张卡片中随机抽取一张，将所得数字作为的值，两次结果记为.

    (1)请你帮他们用画树状图或列表的方法表示所有可能出现的结果;

    (2)若将记录结果看成平面直角坐标系中的一点，求是第一象限内的点的概率.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

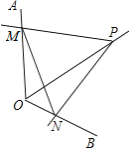
    【题目】如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（　　）

    A. 4B. 3C. 2D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一节数学课后，老师布置了一道课后练习题：

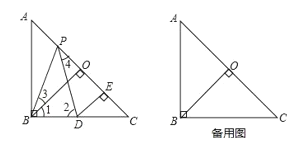
    如图，已知在Rt△ABC中，AB=BC，∠ABC=90°，BO⊥AC于点O，点P、D分别在AO和BC上，PB=PD，DE⊥AC于点E，求证：△BPO≌△PDE．

    理清思路，本题证明的思路可用下列框图表示：

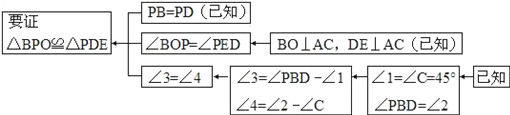
    根据上述思路，请你完成下列问题．

    （1）若BP平分∠ABO，其余条件不变．求证：AP=CD．

    （2）若点P是一个动点，点P运动到OC的中点P′时，满足题中条件的点D也随之在直线BC上运动到点D′，请直接写出CD′与AP′的数量关系,并证明得出的关系.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】3月5日是学雷锋日，也是中国青年志愿者服务日．今年3月5日，某中学组织全体学生参加了“青年志愿者”活动，活动分为“打扫街道(记为A)”“去敬老院服务(记为B)”“到社区文艺演出(记为C)”三项．

    (1)八年级计划在3月5日这天随机完成“青年志愿者”活动中的一项，求八年级完成的恰好是“去敬老院服务”的概率；

    (2)九年级计划在3月5日这天随机完成“青年志愿者”活动中的两项，请用列表或画树状图法求九年级完成的恰好是“打扫街道”和“去敬老院服务”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数（h为常数），在自变量的值满足的情况下，与其对应的函数值的最大值为0，则的值为（ ）

    A. 和B. 和C. 和D. 和

    查看答案和解析>>

    同步练习册答案