
【题目】如图,一次函数与反比例函数的图像交于A(1,12)和B(6,2)两点.点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图像于点M、N,则四边形PMON面积的最大值是 . 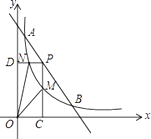
【答案】![]()
【解析】解:设反比例函数解析式为y= ![]() ,一次函数解析式为y=kx+b, 由已知得:12=
,一次函数解析式为y=kx+b, 由已知得:12= ![]() 和
和 ![]() ,
,
解得:m=12和 ![]() .
.
∴一次函数解析式为y=﹣2x+14,反比例函数解析式为y= ![]() .
.
∵点P在线段AB上,
∴设点P的坐标为(n,﹣2n+14)(1<n<6).
令x=n,则y= ![]() ;
;
令y=﹣2n+14,则 ![]() =﹣2n+14,解得:x=
=﹣2n+14,解得:x= ![]() .
.
∴点M(n, ![]() ),点N(
),点N( ![]() ,﹣2n+14).
,﹣2n+14).
S四边形PMON=S矩形OCPD﹣S△ODN﹣S△OCM=n(﹣2n+14)﹣ ![]() n
n ![]() ﹣
﹣ ![]()
![]() (﹣2n+14)=﹣2n2+14n﹣12=﹣2
(﹣2n+14)=﹣2n2+14n﹣12=﹣2 ![]() +
+ ![]() .
.
∴当n= ![]() 时,四边形PMON面积最大,最大面积为
时,四边形PMON面积最大,最大面积为 ![]() .
.
故答案为: ![]() .
.
由点A、B的坐标利用待定系数法即可求出一次函数与反比例函数的解析式,设出点P的坐标为(n,﹣2n+14)(1<n<6).由反比例的函数解析式表示出来M、N点的坐标,分割矩形OCPD,结合矩形和三角形的面积公式即可得出结论.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】一个质地均匀的小正方体,六个面分别标有数字“1”“2”“3”“4”“5”“6”.连续两次抛掷小正方体,观察每次朝上一面的数字.
(1)请用列表格或画树状图的方法列举出两次抛掷的所有可能结果;
(2)求出第二次抛掷的数字大于第一次抛掷的数字的概率;
(3)求两次抛掷的数字之和为5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积. 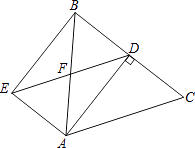
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以线段AC为对角线的四边形ABCD(它的四个顶点A、B、C、D按顺时针方向排列),已知AB=BC=CD,∠ABC=100°,∠CAD=40°;则∠BCD的大小为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是安装在斜屋面上的热水器,图2是安装该热水器的侧面示意图.已知,斜屋面的倾斜角为25°,长为2.1米的真空管AB与水平线AD的夹角为40°,安装热水器的铁架水平横管BC长0.2米,求 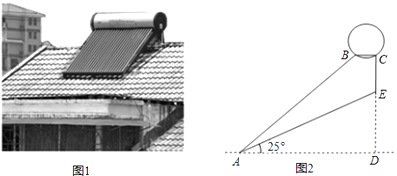
(1)真空管上端B到AD的距离(结果精确到0.01米);
(2)铁架垂直管CE的长(结果精确到0.01米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点P(3a,a)是反比例函数y= ![]() (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
A.y= ![]()
B.y= ![]()
C.y= ![]()
D.y= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.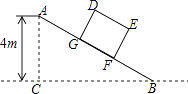
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2a、宽为2b的长方形(其中a,b均为正数,且a>b),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.
(1)你认为图2中大正方形的边长为 a+b ;小正方形(阴影部分)的边长为 .(用含a、b的代数式表示)
(2)仔细观察图2,请你写出下列三个代数式:(a+b)2,(a-b)2,ab所表示的图形面积之间的相等关系,并选取适合a、b的数值加以验证.
(3)已知a+b=7,ab=6.求代数式(a-b)的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com