
【题目】如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE= ![]() ∠A.
∠A. 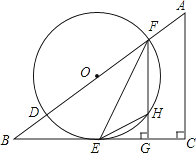
(1)求证:BC是⊙O的切线;
(2)若sinB= ![]() ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
【答案】
(1)
证明:连接OE,
∵在△ABC中,∠C=90°,FG⊥BC,
∴∠BGF=∠C=90°,
∴FG∥AC,
∴∠OFG=∠A,
∴∠OFE= ![]() ∠OFG,
∠OFG,
∴∠OFE=∠EFG,
∵OE=OF,
∴∠OFE=∠OEF,
∴∠OEF=∠EFG,
∴OE∥FG,
∴OE⊥BC,
∴BC是⊙O的切线
(2)
解:∵在Rt△OBE中,sinB= ![]() ,⊙O的半径为r,
,⊙O的半径为r, 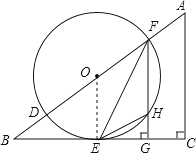
∴OB= ![]() r,BE=
r,BE= ![]() r,
r,
∴BF=OB+OF= ![]() r,
r,
∴FG=BFsinB= ![]() r,
r,
∴BG= ![]() =
= ![]() r,
r,
∴EG=BG﹣BE= ![]() r,
r,
∴S△FGE= ![]() EGFG=
EGFG= ![]() r2,EG:FG=1:2,
r2,EG:FG=1:2,
∵BC是切线,
∴∠GEH=∠EFG,
∵∠EGH=∠FGE,
∴△EGH∽△FGE,
∴ ![]() =(
=( ![]() )=
)= ![]() ,
,
∴S△EHG= ![]() S△FGE=
S△FGE= ![]() r2.
r2.
【解析】(1)首先连接OE,由在△ABC中,∠C=90°,FG⊥BC,可得FG∥AC,又由∠OFE= ![]() ∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;
∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;
(2)由在△OBE中,sinB= ![]() ,⊙O的半径为r,可求得OB,BE的长,然后由在△BFG中,求得BG,FG的长,则可求得EG的长,易证得△EGH∽△FGE,然后由相似三角形面积比等于相似比的平方,求得答案.此题考查了切线的判定、相似三角形的判定与性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.
,⊙O的半径为r,可求得OB,BE的长,然后由在△BFG中,求得BG,FG的长,则可求得EG的长,易证得△EGH∽△FGE,然后由相似三角形面积比等于相似比的平方,求得答案.此题考查了切线的判定、相似三角形的判定与性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】材料阅读:若一个整数能表示成a2+b2(a、b是正整数)的形式,则称这个数为“完美数”.例如:因为13=32+22,所以13是“完美数”;再如:因为a2+2ab+2b2=(a+b)2+b2(a、b是正整数),所以a2+2ab+2b2也是“完美数”.
(1)请你写出一个大于20小于30的“完美数”,并判断53是否为“完美数”;
(2)试判断(x2+9y2)·(4y2+x2)(x、y是正整数)是否为“完美数”,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+b的图象与反比例函数y= ![]() (k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
(k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1). 
(1)求反比例函数的表达式和a、b的值;
(2)若A、O两点关于直线l对称,请连接AO,并求出直线l与线段AO的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)在△BED中作BD边上的高,垂足为F;
(2)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( ) 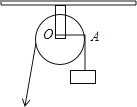
A.πcm
B.2πcm
C.3πcm
D.5πcm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠DCA的平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
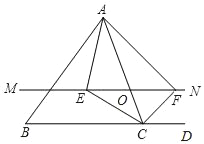
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ![]() ,1)在反比例函数y=
,1)在反比例函数y= ![]() 的图象上.
的图象上. 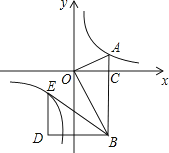
(1)求反比例函数y= ![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP= ![]() S△AOB , 求点P的坐标;
S△AOB , 求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)在线段AB上找一点P,连结FP使FP⊥AC,连结PC,试判定四边形APCF的形状,并说明理由,直接写出此时线段PF的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com