
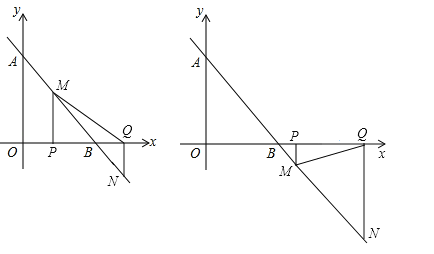
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��ͼ����y��������ύ�ڵ�A����x�ύ�ڵ�B��2��0������������ABO�����Ϊ2������P�ӵ�O��������ÿ��1����λ���ȵ��ٶ�������OB���˶�������Q��B��������x������������Pͬʱ����ͬ���ٶ��˶�����P��PM��X�ύֱ��AB��M��

��1����ֱ��AB�Ľ���ʽ��
��2������P���˶�ʱ������MPQ�����ΪS����P�˶���ʱ��Ϊt�룬��S��t�ĺ�����ϵʽ��ֱ��д���Ա�����ȡֵ��Χ����
��3������Q��QN��X�ύֱ��AB��N�����˶������У�P����B�غϣ����Ƿ����ijһʱ��t���룩��ʹ��MNQ�ǵ��������Σ������ڣ����ʱ��tֵ��
���𰸡���1��ֱ��AB�Ľ���ʽΪy=��x+2����2��t=![]() ��4ʱ����MNQ�ǵ��������Σ�
��4ʱ����MNQ�ǵ��������Σ�
�������������������1�����������ε�������OA����д����A�����꣬Ȼ�����ô���ϵ������һ�κ�������ʽ���
��2�����ݵ���ֱ�������ε����ʱ�ʾ��PM�������PQ�ij���Ȼ������ֱ�������ε������ʽ��ʽ�������ɵý⣻
��3����ʾ��PM��QN�������ù��ɶ�����ʽ��ʾ��QM2�������MN��Ȼ���MN=QN��MN=QM��QN=QM��������г�������⼴�ɣ�
����������⣺��1������B��2��0������OB=2����S��ABO=![]() OBOA=
OBOA=![]() ��2OA=2�����OA=2������A��0��2������ֱ��AB�Ľ���ʽΪy=kx+b������
��2OA=2�����OA=2������A��0��2������ֱ��AB�Ľ���ʽΪy=kx+b������ ![]() �������
������� ![]() ����ֱ��AB�Ľ���ʽΪy=��x+2��
����ֱ��AB�Ľ���ʽΪy=��x+2��
��2����OA=OB=2�����ABO�ǵ���ֱ�������Σ�����P��Q���ٶȶ���ÿ��1����λ���ȣ���PM=PB=OB��OP=2��t��PQ=OB=2�����MPQ�����ΪS=![]() PQPM=
PQPM=![]() ��2����2��t��=2��t������P���߶�OB���˶�����0��t��2����S��t�ĺ�����ϵʽΪS=2��t��0��t��2����
��2����2��t��=2��t������P���߶�OB���˶�����0��t��2����S��t�ĺ�����ϵʽΪS=2��t��0��t��2����
��3��t��ʱ��PM=PB=|2��t|��QN=BQ=t�����ԣ�QM2=PM2+PQ2=��2��t��2+4��MN=![]() ��QN��PM��=
��QN��PM��=![]() ��t��t��2��=
��t��t��2��=![]() ��
��
����MN=QN����t=![]() ��
��
����MN=QM����2��t��2+4=��![]() ��2�������ã�t2��4t=0�����t1=0����ȥ����t2=4��
��2�������ã�t2��4t=0�����t1=0����ȥ����t2=4��
����QN=QM����2��t��2+4=t2�����ã�4t��8=0�����t=2����ʱ��P�����B�غϣ�����������ȥ��
����������t=![]() ��4ʱ����MNQ�ǵ��������Σ�
��4ʱ����MNQ�ǵ��������Σ�


 Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʽy=ax3+bx+c�У���x=0ʱ��y=3����x=��1ʱ��y=5����x=1ʱ��y��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѡ���������߶�����������ε��ǣ��� ����
A.5cm��6cm��13cmB.3cm��3cm��6cmC.4cm��5cm��6cmD.4cm��29cm��11cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ڡ�ABC�У���C=90�㣬AC=6��BC=8��M��BC���е㣬PΪAB�ϵ�һ�����㣨��������A��B�غϣ���������MPD=90�㣬PD��BC����BC���ӳ��ߣ��ڵ�D
��1����BP�ij�Ϊx����BPM�����Ϊy����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2���Ƿ���������ĵ�P��ʹ�á�MPD���ABC���ƣ������ڣ������x��ֵ���������ڣ���˵������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȫ���������ԼΪ36105.9��ƽ������ÿ�ѧ��������ʾΪ�� ��
A.3.61��108ƽ������
B.3.60��108ƽ������
C.361��106ƽ������
D.36100��ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=��![]() ��x+4��
��x+4��
��1�����䷽��ȷ�����Ķ������ꡢ�Գ��
��2��xȡ��ֵʱ��y��x�������С��
��3��xȡ��ֵʱ����������x���Ϸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������6��װ���ǹ�������У�ÿ����������ִ���������ʵ��װ�е��ǹ��������������е�5����������С�Һ�С�죬�Լ�����1�У���֪�͵Ķ������У���װû�������С�ҵ��ǹ�������С���2�����������Լ����µ�������ǹ���������
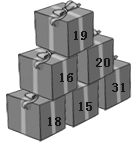
A. 15�� B. 18�� C. 20�� D. 31��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������һ��У�����������Ļ���ΧŨ����ռ��70��Ķ���������Լ5��ƽ���ף��뽫5��ƽ����������ÿ�ѧ��������ʾ�� ��
A.5.0��105ƽ����
B.5.0��104ƽ����
C.50��103ƽ����
D.0.5��106ƽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ĸ�BD��CE�ཻ�ڵ�O����������һ��������ʹBD=CE���������ӵ�������________����������һ����ȵ��߶λ�һ����ȵĽǣ�
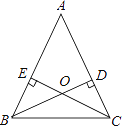
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com