
分析 (1)令y=0,使得二次函数变为一元二次方程,然后求出方程中△的值,即可证明结论;
(2)令y=0,使得二次函数变为一元二次方程,然后对方程分解因式,又因此二次函数的图象与x轴两个交点的横坐标都是整数,从而可以求得符合要求的正整数m的值.
解答 解:(1)证明:∵二次函数y=mx2-(m+2)x+2(m≠0),
∴当y=0时,0=mx2-(m+2)x+2(m≠0),
△=[-(m+2)]2-4×m×2=m2+4m+4-8m=m2-4m+4=(m-2)2≥0
∴0=mx2-(m+2)x+2(m≠0)有两个实数根,
即二次函数y=mx2-(m+2)x+2(m≠0)的图象与x轴总有交点;
(2)∵二次函数y=mx2-(m+2)x+2(m≠0),
∴当y=0时,0=mx2-(m+2)x+2=(mx-2)(x-1),
∴${x}_{1}=\frac{2}{m},{x}_{2}=1$,
又∵此二次函数的图象与x轴两个交点的横坐标都是整数,
∴正整数m的值是:1或2,
即正整数m的值是1或2.
点评 本题考查抛物线与x轴的交点,解题的关键是建立二次函数与一元二次方程之间的关系,然后找出所求问题需要的条件.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
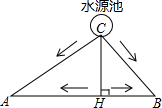 如图所示,A、B两块试验田相距200米,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.
如图所示,A、B两块试验田相距200米,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com