
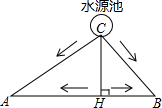
 如图所示,A、B两块试验田相距200米,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.
如图所示,A、B两块试验田相距200米,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.分析 (1)由勾股定理的逆定理即可得出△ABC是直角三角形;
(2)由△ABC的面积求出CH,得出AC+BC<CH+AH+BH,即可得出结果.
解答 解:(1)△ABC是直角三角形;理由如下:
∴AC2+BC2=1602+1202=40000,AB2=2002=40000,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
(2)甲方案所修的水渠较短;理由如下:
∵△ABC是直角三角形,
∴△ABC的面积=$\frac{1}{2}$AB•CH=$\frac{1}{2}$AC•BC,
∴CH=$\frac{AC•BC}{AB}$=$\frac{160×120}{200}$=96(m),
∵CH⊥AB,
∴∠AHC=90°,
∴AH=$\sqrt{A{C}^{2}-C{H}^{2}}$=$\sqrt{16{0}^{2}-9{6}^{2}}$=128(m),
∴BH=AB-AH=72m,
∵AC+BC=160m+120m=280m,CH+AH+BH=96m+200m=296m,
∴AC+BC<CH+AH+BH,
∴甲方案所修的水渠较短.
点评 本题考查了勾股定理的应用、勾股定理的逆定理、三角形面积的计算;熟练掌握勾股定理,由勾股定理的逆定理证出△ABC是直角三角形是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
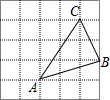 如图,每个小方格都是边长为1个单位的小正方形,A,B,C三点都是格点(每个小方格的顶点叫格点).
如图,每个小方格都是边长为1个单位的小正方形,A,B,C三点都是格点(每个小方格的顶点叫格点).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相切 | B. | 相离 | C. | 相交 | D. | 相切或相交 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com