
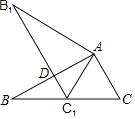
【题目】如图,将△ABC绕顶点A顺时针旋转60°后得到△AB1C1,且C1为BC的中点,AB与B1C1相交于D,若AC=2,则线段B1D的长度为_____.
【答案】3.
【解析】
由旋转的性质可得AC=AC1,∠AC1B1=∠C=60°,可证△ACC1为等边三角形,可得BC1=CC1=AC=2,可证∠B=∠C1AB=30°,由含30°的直角三角形的性质可求解.
解:根据旋转的性质可知:AC=AC1,∠AC1B1=∠C=60°,
∵旋转角是60°,即∠C1AC=60°,
∴△ACC1为等边三角形,
又C1为BC的中点,
∴BC1=CC1=AC=AC1=2,
∴∠B=∠C1AB=30°,
∴∠BDC1=∠C1AB+∠AC1B1=90°,
∴BC1=2C1D,
∴C1D=1,
∴BC=B1C1=BC1+CC1=4,
∴B1D=B1C1 -C1D=3,
故答案为:3.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 轴正半轴上,抛物线
轴正半轴上,抛物线![]() 经过
经过![]() 、
、![]() 两点,连接
两点,连接![]() ,
,![]() .
.
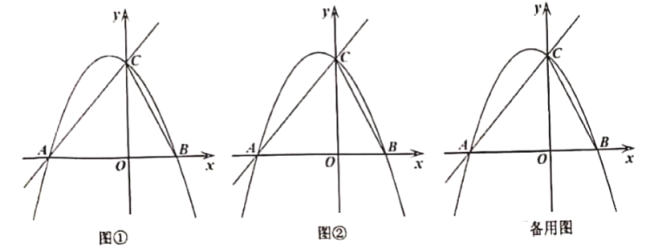
(1)求抛物线的解析式:
(2)点![]() 在第二象限的抛物线上,过点
在第二象限的抛物线上,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)在(2)的条件下,若点![]() 和点
和点![]() 同在一个象限内,连接
同在一个象限内,连接![]() 、
、![]() ,
,![]() ,求
,求![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
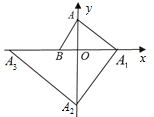
【题目】如图,在平面直角坐标系中点A(0,3),![]() ,过点A作AB的垂线交x轴于点A1,过A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3……,按此规律继续作下去,直至得到点A2018为止,则点A2018坐标为__________.
,过点A作AB的垂线交x轴于点A1,过A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3……,按此规律继续作下去,直至得到点A2018为止,则点A2018坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC于点D,点E为BC的中点,连接DE.

(1)求证:DE是半圆⊙O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市中招体育测试改革,其中篮球和足球作为选考项目,某商店抓住这一商机决定购进一批篮球和足球共200个,这两种球的进价和售价如下表所示:
篮球 | 足球 | |
进价(元/个) | 180 | 150 |
售价(元/个) | 250 | 200 |
(1)若商店计划销售完这批球后能获利11600元,问篮球和足球应分别购进多少个?
(2)设购进篮球![]() 个,获利为
个,获利为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系;
之间的函数关系;
(3)若商店计划投入资金不多于31560元且销售完这批球后商店获利不少于11000元,请问有哪几种购球方案,并写出获利最大的购球方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
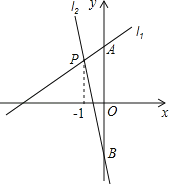
【题目】如图,直线l1与l2相交于点P,点P横坐标为﹣1,l1的解析式为y=![]() x+3,且l1与y轴交于点A,l2与y轴交于点B,点A与点B恰好关于x轴对称.
x+3,且l1与y轴交于点A,l2与y轴交于点B,点A与点B恰好关于x轴对称.
(1)求点B的坐标;
(2)求直线l2的解析式;
(3)若点M为直线l2上一动点,直接写出使△MAB的面积是△PAB的面积的![]() 的点M的坐标;
的点M的坐标;
(4)当x为何值时,l1,l2表示的两个函数的函数值都大于0?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成图1的条形统计图和图2扇形统计图,但均不完整.请你根据统计图解答下列问题:
(1)求参加比赛的学生共有多少名?并补全图1的条形统计图.
(2)在图2扇形统计图中,m的值为_____,表示“D等级”的扇形的圆心角为_____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务.
三等分任意角问题是数学史上一个著名的问题,直到1837年,数学家才证明了“三等分任意角”是不能用尺规完成的.
在探索中,出现了不同的解决问题的方法
方法一:
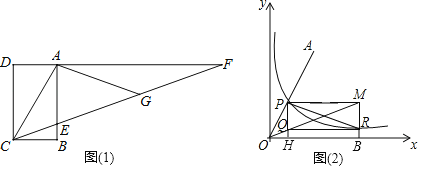
如图(1),四边形ABCD是矩形,F是DA延长线上一点,G是CF上一点,CF与AB交于点E,且∠ACG=∠AGC,∠GAF=∠F,此时∠ECB=![]() ∠ACB.
∠ACB.
方法二:
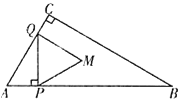
数学家帕普斯借助函数给出一种“三等分锐角”的方法(如图(2)):将给定的锐角∠AOB置于平面直角坐标系中,边OB在x轴上,边OA与函数y=![]() 的图象交于点P,以点P为圆心,以2OP长为半径作弧交图象于点R.过点P作x轴的平行线,过点R作y轴的平行线,两直线相交于点M,连接OM得到∠AOB,过点P作PH⊥x轴于点H,过点R作RQ⊥PH于点Q,则∠MOB=
的图象交于点P,以点P为圆心,以2OP长为半径作弧交图象于点R.过点P作x轴的平行线,过点R作y轴的平行线,两直线相交于点M,连接OM得到∠AOB,过点P作PH⊥x轴于点H,过点R作RQ⊥PH于点Q,则∠MOB=![]() ∠AOB.
∠AOB.
(1)在“方法一”中,若∠ACF=40°,GF=4,求BC的长.
(2)完成“方法二”的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发以每秒2个单位的速度沿
出发以每秒2个单位的速度沿![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 的垂线交折线
的垂线交折线![]() 于点
于点![]() ,当点
,当点![]() 不和
不和![]() 的顶点重合时,以
的顶点重合时,以![]() 为边作等边三角形
为边作等边三角形![]() ,使点
,使点![]() 和点
和点![]() 在直线
在直线![]() 的同侧,设点
的同侧,设点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
(1)求等边三角形![]() 的边长(用含
的边长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 的边
的边![]() 上时,求
上时,求![]() 的值;
的值;
(3)设![]() 与
与![]() 重合部分图形的面积为
重合部分图形的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)作直线![]() ,设点
,设点![]() 关于直线
关于直线![]() 的对称点分别为
的对称点分别为![]() ,直接写出
,直接写出![]() 时
时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com