
某市民营经济持续发展,2013年城镇民营企业就业人数突破20万.为了解城镇民营企业员工每月的收入状况,统计局对全市城镇民营企业员工2013年月平均收入随机抽样调查,将抽样的数据按“2000元以内”、“2000元~4000元”、“4000元~6000元”和“6000元以上”分为四组,进行整理,分别用A,B,C,D表示,得到下列两幅不完整的统计图.

由图中所给出的信息解答下列问题:
(1)本次抽样调查的员工有 人,在扇形统计图中 的值为 ,表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是 ;
的值为 ,表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是 ;
(2)将不完整的条形图补充完整,并估计该市2013年城镇民营企业20万员工中,每月的收入在“2000元~4000元”的约有多少人?
(1)500,14,21.6°;(2)12万
【解析】
试题分析:(1)用B的人数除以所占的百分比,计算即可求出被调查的员工总人数,求出B所占的百分比得到x的值,再求出A所占的百分比,然后乘以360°计算即可得解;
(2)求出C的人数,然后补全统计图即可,再用总人数乘以B所占的百分比计算即可得解;
试题解析:(1)本次抽样调查的员工人数是: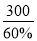 =500(人),
=500(人),
D所占的百分比是: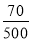 ×100%=14%,
×100%=14%,
则在扇形统计图中x的值为14;
“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是360°×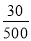 =21.6°;
=21.6°;
故答案为:500,14,21.6°;
(2)C的人数为:500×20%=100,
补全统计图如图所示,
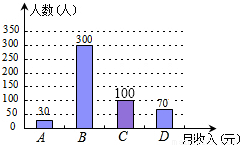
“2000元~4000元”的约为:20万×60%=12万;
考点:1.条形统计图;2.用样本估计总体;3.扇形统计图;4.加权平均数


科目:初中数学 来源:2014-2015学年广东省广州市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分14分)如图①,在平面直角坐标系中,点 的坐标为
的坐标为 ,点
,点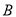 的坐标为
的坐标为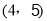 ,二次函数
,二次函数 的图象记为抛物线
的图象记为抛物线 .
.

(1)平移抛物线 ,使平移后的抛物线过
,使平移后的抛物线过 两点,记为抛物线
两点,记为抛物线 ,如图②,求抛物线
,如图②,求抛物线 的函数表达式.
的函数表达式.
(2)请在图②上用尺规作图的方式探究抛物线 上是否存在点
上是否存在点 ,使
,使 为等腰三角形.若存在,请判断点
为等腰三角形.若存在,请判断点 共有几个可能的位置(保留作图痕迹)并在图中画出P点,以P1、P2、P3、、、表示不同的点;若不存在,请说明理由.
共有几个可能的位置(保留作图痕迹)并在图中画出P点,以P1、P2、P3、、、表示不同的点;若不存在,请说明理由.
(3)设抛物线 的顶点为
的顶点为 ,
, 为抛物线
为抛物线 一点.若
一点.若 ,求点
,求点 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,AB是⊙O的直径,C.D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
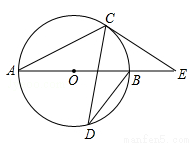
(A)40° (B)50° (C)60° (D)70°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市九年级上学期综合测试一数学试卷(解析版) 题型:解答题
如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)对角线AC的长是 ,菱形ABCD的面积是 ;
(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由;
(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由,若变化,请探究OE、OF之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市九年级上学期综合测试一数学试卷(解析版) 题型:填空题
已知线段CD是由线段AB平移得到的,点A(﹣1,4)的对应点为C(4,7),则点B(﹣4,﹣1)的对应点D的坐标为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市九年级上学期综合测试一数学试卷(解析版) 题型:选择题
用10米长的铝材制成一个矩形窗框,使它的面积为6平方米.若设它的一条边长为x米,则根据题意可列出关于x的方程是( ).
(A) (B)
(B)
(C) (D)
(D)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市长泾片七年级上学期期中考试数学试卷(解析版) 题型:填空题
已知4x2mym+n与3x6y2是同类项,则m-n=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知射线CB∥OA,∠C=∠OAB=140°,E、F在CB上,且满足OB平分∠AOF,OE平分∠COF
【小题1】求∠EOB的度数。
【小题2】若平行移动AB,那么∠OBC︰∠OFC的值是否随之发生变化?若变化,找出变化规律;若不变,求出这个值。
【小题3】在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,请求出∠OEC和∠OBA的度数;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com