
(本题满分14分)如图①,在平面直角坐标系中,点 的坐标为
的坐标为 ,点
,点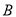 的坐标为
的坐标为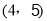 ,二次函数
,二次函数 的图象记为抛物线
的图象记为抛物线 .
.

(1)平移抛物线 ,使平移后的抛物线过
,使平移后的抛物线过 两点,记为抛物线
两点,记为抛物线 ,如图②,求抛物线
,如图②,求抛物线 的函数表达式.
的函数表达式.
(2)请在图②上用尺规作图的方式探究抛物线 上是否存在点
上是否存在点 ,使
,使 为等腰三角形.若存在,请判断点
为等腰三角形.若存在,请判断点 共有几个可能的位置(保留作图痕迹)并在图中画出P点,以P1、P2、P3、、、表示不同的点;若不存在,请说明理由.
共有几个可能的位置(保留作图痕迹)并在图中画出P点,以P1、P2、P3、、、表示不同的点;若不存在,请说明理由.
(3)设抛物线 的顶点为
的顶点为 ,
, 为抛物线
为抛物线 一点.若
一点.若 ,求点
,求点 的坐标.
的坐标.
(1)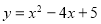 (2)5个 (3)(3,2)
(2)5个 (3)(3,2)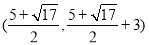
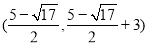
【解析】
试题分析:(1)可设出平移后的二次函数的解析式,然后将A、B的坐标代入抛物线的解析式中,即可求得l2的函数表达式.
(2)应有三点:①以A为圆心,AB为半径作弧可交抛物线l2于一点;②以B为圆心,AB为半径坐标交抛物线于另一点;③作线段AB的垂直平分线可交抛物线于两点,因此共有5个符合条件的P点.
(3)第一种情况:根据函数的对称性可以求出K点.
第二种情况:本题可通过求三角形的面积来求K的坐标.由于三角形ABC的面积无法直接求出,因此可其转换成其他规则图形面积的和差来解.分别过A、B、C三点作x轴的垂线,因此△ABC的面积可用三个直角梯形的面积差来求出.设出K的坐标,利用上面面积求法求出K的坐标.
试题解析:(1) 设抛物线l2的函数表达式为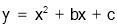 ,
,
把A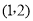 ,B
,B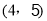 代入得
代入得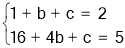
解之得b=-4,c=5
所以 的解析式为
的解析式为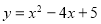 .
.
(2) 由题意可做图为
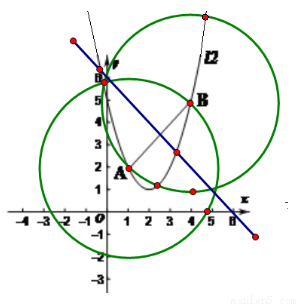
由图可以直接看出共5个点.
(3)第一种情况:因为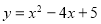 ,所以可求出顶点C的坐标为(2,1),根据二次函数的对称性可以知当K点和A点对称时两个三角形的面积相等,由对称轴x=2可求得K点的横坐标为3,所以K的坐标为(3,2).
,所以可求出顶点C的坐标为(2,1),根据二次函数的对称性可以知当K点和A点对称时两个三角形的面积相等,由对称轴x=2可求得K点的横坐标为3,所以K的坐标为(3,2).
第二种情况:

由函数的解析式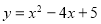 可求出C的坐标(2,1),然后过ABC作垂线(如图),利用梯形的面积差可以求出
可求出C的坐标(2,1),然后过ABC作垂线(如图),利用梯形的面积差可以求出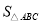 =3,设K点为(x,y),同理可用面积法求出K点的坐标为
=3,设K点为(x,y),同理可用面积法求出K点的坐标为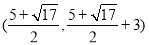 和
和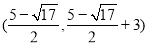 ,所以有三种情况,分别为(3,2)
,所以有三种情况,分别为(3,2)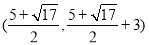
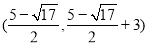 .
.
考点:二次函数的图像和性质,梯形的面积,基本作图


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源:2014-2015学年广东省汕头市九年级上学期第一次阶段质量检测数学试卷(解析版) 题型:解答题
x取什么值时,代数式x2+8x-12的值等于2x2+x的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省八年级上学期期中数学试卷(解析版) 题型:填空题
原点O的坐标是 ; 在电影票上,如果将“8排4号”记作(8,4),
那么(10,15)表示______________________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分10分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A( ,
, )、B(
)、B( ,1)、C(0,
,1)、C(0, ).
).

(1) 点B关于坐标原点O对称的点的坐标为__________;
(2) 将△ABC绕点C顺时针旋转 ,画出旋转后得到的△A1B1C;
,画出旋转后得到的△A1B1C;
(3) 求过点B1的反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市九年级上学期综合测试一数学试卷(解析版) 题型:解答题
某市民营经济持续发展,2013年城镇民营企业就业人数突破20万.为了解城镇民营企业员工每月的收入状况,统计局对全市城镇民营企业员工2013年月平均收入随机抽样调查,将抽样的数据按“2000元以内”、“2000元~4000元”、“4000元~6000元”和“6000元以上”分为四组,进行整理,分别用A,B,C,D表示,得到下列两幅不完整的统计图.

由图中所给出的信息解答下列问题:
(1)本次抽样调查的员工有 人,在扇形统计图中 的值为 ,表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是 ;
的值为 ,表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是 ;
(2)将不完整的条形图补充完整,并估计该市2013年城镇民营企业20万员工中,每月的收入在“2000元~4000元”的约有多少人?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市长泾片九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,P是双曲线y= (x>0)的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与直线y=3相切时,点P的坐标为 .
(x>0)的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与直线y=3相切时,点P的坐标为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com