
【题目】已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD ≌ △EOC;
(2)连接AC,DE,当∠B![]() ∠AEB
∠AEB![]() _______ °时,四边形ACED是正方形?请说明理由.
_______ °时,四边形ACED是正方形?请说明理由.
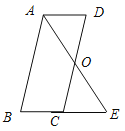
【答案】(1)证明见解析(2)当∠B=∠AEB=45°时,四边形ACED是正方形
【解析】试题分析:(1)根据平行线的性质可得∠D=∠OCE,∠DAO=∠E,再根据中点定义可得DO=CO,然后可利用AAS证明△AOD≌△EOC;
(2)当∠B=∠AEB=45°时,四边形ACED是正方形,首先证明四边形ACED是平行四边形,再证对角线互相垂直且相等可得四边形ACED是正方形.
试题解析:证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠D=∠OCE,∠DAO=∠E.∵O是CD的中点,∴OC=OD.在△ADO和△ECO中,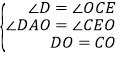 ,∴△AOD≌△EOC(AAS);
,∴△AOD≌△EOC(AAS);
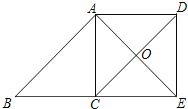
(2)当∠B=∠AEB=45°时,四边形ACED是正方形.
∵△AOD≌△EOC,∴OA=OE.
又∵OC=OD,∴四边形ACED是平行四边形.
∵∠B=∠AEB=45°,∴AB=AE,∠BAE=90°.
∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠COE=∠BAE=90°,∴ACED是菱形.∵AB=AE,AB=CD,∴AE=CD,∴菱形ACED是正方形.
故答案为:45.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=15cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒

当t = 4时,求线段PQ的长度
(2)当t为何值时,△PCQ是等腰三角形?
(3)当t为何值时,△PCQ的面积等于16cm2?
(4)当t为何值时,△PCQ∽△ACB
查看答案和解析>>
科目:初中数学 来源: 题型:
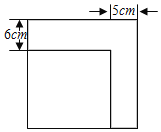
【题目】如图,小刚将一个正方形纸片剪去一个宽为5cm的长条后,再从剩下的长方形纸片上剪去一个宽为6cm的长条.如果两次剪下的长条面积正好相等,求两个所剪下的长条的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:﹣32+|2﹣5|÷![]() +(﹣2)3×(﹣1)2015
+(﹣2)3×(﹣1)2015
(2)解方程:![]() ﹣
﹣![]() =3.
=3.
(3)解方程:6(x-2)=8x+3.
(4)解方程: x-![]() =2-
=2-![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
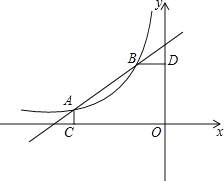
【题目】如图,在平面直角坐标系中,直线y=![]() x+
x+![]() 与反比例函数y=
与反比例函数y=![]() (x<0)的图象交于A(-4,a)、B(-1,b)两点,AC⊥x轴于C,BD⊥y轴于D.
(x<0)的图象交于A(-4,a)、B(-1,b)两点,AC⊥x轴于C,BD⊥y轴于D.
(1)求a 、b及k的值;
(2)连接OA,OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
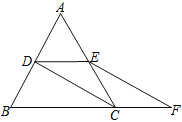
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连结CD和EF.
BC,连结CD和EF.
(1)求证:四边形CDEF是平行四边形;
(2)求四边形BDEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54,则∠B=( )

A. 54 B. 60 C. 72 D. 66
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:
(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有( )

A.2个 B.3个 C.4个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E.
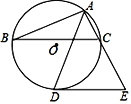
(1)试判断DE与⊙O的位置关系,并证明你的结论;
(2)若∠E=60°,⊙O的半径为5,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com