
【题目】已知抛物线C1:y=﹣ ![]() x2+bx+c的对称轴是x=2,且经过点(6,0).
x2+bx+c的对称轴是x=2,且经过点(6,0).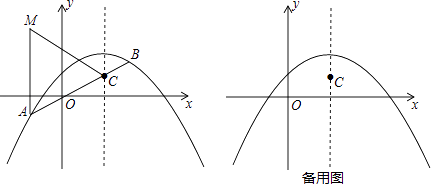
(1)求抛物线C1的解析式;
(2)将抛物线C1向下平移2个单位后得到抛物线C2 , 如图,直线y=kx﹣2k+1交抛物线C2于A,B两点(点A在点B的左边),交抛物线C2的对称轴于点C,M(xA , 3),xA表示点A横坐标,求证:AC=AM;
(3)在(2)的条件下,请你参考(2)中的结论解决下列问题:
①若CM=AM,求 ![]() 的值;
的值;
②请你探究:在抛物线C2上是否存在点P,使得PO+PC取得最小值?如果存在,求出点P的坐标;如果不存在,请说明理由.
【答案】
(1)解:∵抛物线C1的对称轴为直线x=2,且抛物线与x轴的一个交点坐标为(6,0),
∴抛物线与x轴的另一个交点坐标为(﹣2,0),
∴抛物线C1的解析式为y=﹣ ![]() (x+2)(x﹣6),
(x+2)(x﹣6),
即y=﹣ ![]() x2+x+3
x2+x+3
(2)证明:∵抛物线C1的解析式为y=﹣ ![]() (x﹣2)2+4,
(x﹣2)2+4,
∴抛物线C2的解析式为y=﹣ ![]() (x﹣2)2+2,
(x﹣2)2+2,
∵直线y=kx﹣2k+1过定点(2,1),
而直线y=kx﹣2k+1交抛物线C2的对称轴于点C,
∴C(2,1),
设A[x,﹣ ![]() (x﹣2)2+2)],
(x﹣2)2+2)],
∴AC2=(x﹣2)2+[﹣ ![]() (x﹣2)2+2﹣1]2=
(x﹣2)2+2﹣1]2= ![]() (x﹣2)4+
(x﹣2)4+ ![]() (x﹣2)2+1,
(x﹣2)2+1,
AM2=[﹣ ![]() (x﹣2)2+2﹣3]2=
(x﹣2)2+2﹣3]2= ![]() (x﹣2)4+
(x﹣2)4+ ![]() (x﹣2)2+1,
(x﹣2)2+1,
∴AC=AM
(3)解:①∵AC=AM,CM=AM,
∴△ACM是等边三角形.
∴∠AMC=∠ACM=60°,
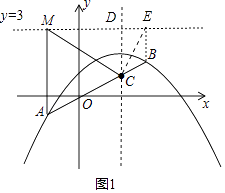
直线y=3交直线x=2于D点,过点B作BE⊥直线y=3于点E,如图1,则由(2)可知BC=BE,易证∠MCD=60°,∠BCE=∠DCE=30°,
在Rt△CDE中,tan∠DCE=tan30°= ![]() =
= ![]() ,
,
在Rt△CDM中,tan∠CMD=tan30°= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵AM∥DC∥EB,
∴ ![]() =
= ![]() =
= ![]() ;
;
②存在.
如图2,y轴与抛物线的交点记作点P,与直线y=3的交点记作点H,
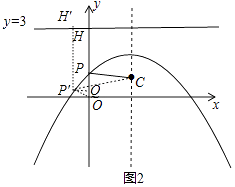
由(2)可知PC=PH,
如图,在抛物线上取异于点P的P′,作P′H′⊥直线y=3于H′,P′Q⊥y轴于点Q,
由(2)可知P′C=PH′,
易得四边形HH′P′Q为矩形,
∴P′H′=QH,
∵OP′>OQ,
∴OQ+QH<OP′+P′H′,
∴OP+PH<OP′+P′C,
∴点P(0,1)使得PO+PC取得最小值.
【解析】(1)根据已知点的坐标和对称轴求出此抛物线与x轴的另一个交点坐标,即可求出抛物线的解析式。
(2)先抛物线C1写成顶点式,再根据平移规律(上加下减),求出抛物线C2的函数解析式,而交抛物线C2的对称轴于点C,,可知点C(2,1),再设出点A的坐标,利用勾股定理求出AC2、AM2即可得到AC=AM。
(3)①由已知易征得△ACM是等边三角形.直线y=3交直线x=2于D点,过点B作BE⊥直线y=3于点E,在Rt△CDE中和Rt△CDM中,利用解直角三角形得出![]() 、
、![]() 的值,从而得到DE:DM的值,再由AM∥DC∥EB,得出对应线段成比例,即可求得结果;②y轴与抛物线的交点记作点P,与直线y=3的交点记作点H,先证明四边形HH′P′Q为矩形,得到P′H′=QH,再利用OP′>OQ得出OP+PH<OP′+P′C,,于是可判断点P(0,1)使得PO+PC取得最小值。
的值,从而得到DE:DM的值,再由AM∥DC∥EB,得出对应线段成比例,即可求得结果;②y轴与抛物线的交点记作点P,与直线y=3的交点记作点H,先证明四边形HH′P′Q为矩形,得到P′H′=QH,再利用OP′>OQ得出OP+PH<OP′+P′C,,于是可判断点P(0,1)使得PO+PC取得最小值。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】“大美武汉,畅游江城”.某校数学兴趣小组就“最想去的武汉市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:
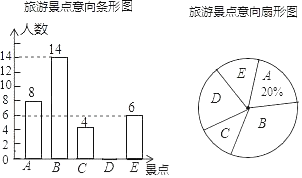
请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有1200名学生,请估计“最想去景点B“的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设M(m,n)在反比例函数y=﹣ ![]() 上,其中m是分式方程
上,其中m是分式方程 ![]() ﹣1=
﹣1= ![]() 的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
A.y=﹣ ![]() x﹣
x﹣ ![]()
B.y= ![]() x+
x+ ![]()
C.y=4x﹣5
D.y=﹣4x+5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题 1、如图1,线段AB的端点在正方形网格的格点上,在图1中找到格点C,使组成的△ABC的一个内角α满足tanα=2(找到两个点C,全等的三角形算一种)
2、
(1)如图1,线段AB的端点在正方形网格的格点上,在图1中找到格点C,使组成的△ABC的一个内角α满足tanα=2(找到两个点C,全等的三角形算一种).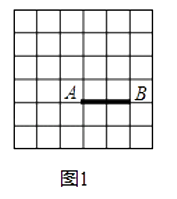
(2)如图2,在Rt△DEF中,∠DEF=90°,DE=1,sin∠F= ![]() .用两块全等的△DEF拼出一个平行四边形,将拼得的平行四边形画在图2网格(网格图中小正方形边长均为1)中,画出不同的两种平行四边形(全等的算一种),并写出相应的周长.
.用两块全等的△DEF拼出一个平行四边形,将拼得的平行四边形画在图2网格(网格图中小正方形边长均为1)中,画出不同的两种平行四边形(全等的算一种),并写出相应的周长.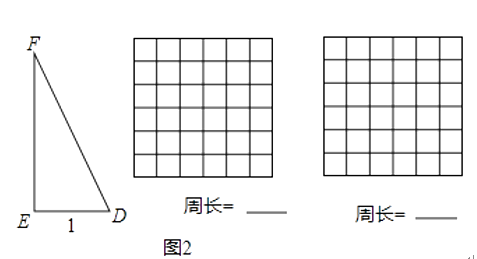
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(或方程组)解应用题:
(1)某服装店到厂家选购甲、乙两种服装,若购进甲种服装9件、乙种服装10件,需1810元;购进甲种服装11件乙种服装8件,需1790元,求甲乙两种服装每件价格相差多少元?
(2)某工厂现库存某种原料1200吨,用来生产A、B两种产品,每生产1吨A产品需这种原料2吨、生产费用1000元;每生产1吨B产品需这种原料2.5吨、生产费用900元,如果用来生产这两种产品的资金为53万元,那么A、B两种产品各生产多少吨才能使库存原料和资金恰好用完?
查看答案和解析>>
科目:初中数学 来源: 题型:
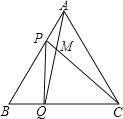
【题目】点P、Q分别是边长为4cm的等边![]() 的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是
的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是![]() ,设运动时间为t秒.
,设运动时间为t秒.
![]() 连接AQ、CP交于点M,则在P、Q运动的过程中,
连接AQ、CP交于点M,则在P、Q运动的过程中,![]() 变化吗:若变化,则说明理由,若不变,则求出它的度数;
变化吗:若变化,则说明理由,若不变,则求出它的度数;
![]() 连接PQ,
连接PQ,
![]() 当
当![]() 秒时,判断
秒时,判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 当
当![]() 时,则
时,则![]() ______秒
______秒![]() 直接写出结果
直接写出结果![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用我们学过的知识,可以导出下面这个形式优美的等式:a2+b2+c2﹣ab﹣bc﹣ac=![]() [(a﹣b)2+(b﹣c)2+(a﹣c)2],该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁、美观.
[(a﹣b)2+(b﹣c)2+(a﹣c)2],该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁、美观.
(1)请你检验说明这个等式的正确性.
(2)若a=2019,b=2020,c=2021,你能很快求出a2+b2+c2﹣ab﹣bc﹣ac的值吗?
(3)若a﹣b=![]() ,b﹣c=
,b﹣c=![]() ,且a2+b2+c2=1,求ab+bc+ac的值.
,且a2+b2+c2=1,求ab+bc+ac的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
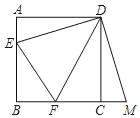
【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D按逆时针方向旋转90°得到△DCM.
(1)求证:EF=MF;(2)当AE=1时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AH是⊙O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为半径OH上一点,点E,F分别在矩形ABCD的边BC和CD上.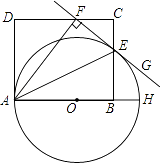
(1)求证:直线FG是⊙O的切线;
(2)若CD=10,EB=5,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com