
【题目】如图,将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3),动点F从点O出发以每秒1个单位长度的速度沿OC向终点C运动,运动![]() 秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)
秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)
(1)OE= ,OF= (用含t的代数式表示)
(2)当t=1时,将△OEF沿EF翻折,点O恰好落在CB边上的点D处
①求点D的坐标及直线DE的解析式;
②点M是射线DB上的任意一点,过点M作直线DE的平行线,与x轴交于N点,设直线MN的解析式为y=kx+b,当点M与点B不重合时,S为△MBN的面积,当点M与点B重合时,S=0.求S与b之间的函数关系式,并求出自变量b的取值范围.

【答案】(1)6-t,![]() +t;(2)①直线DE的解析式为:y=-
+t;(2)①直线DE的解析式为:y=-![]() ;②
;②
【解析】
(1)由O(0,0),A(6,0),C(0,3),可得:OA=6,OC=3,根据矩形的对边平行且相等,可得:AB=OC=3,BC=OA=6,进而可得点B的坐标为:(6,3),然后根据E点与F点的运动速度与运动时间即可用含t的代数式表示OE,OF;
(2)①由翻折的性质可知:△OPF≌△DPF,进而可得:DF=OF,然后由t=1时,DF=OF=![]() ,CF=OC-OF=
,CF=OC-OF=![]() ,然后利用勾股定理可求CD的值,进而可求点D和E的坐标;利用待定系数可得直线DE的解析式;
,然后利用勾股定理可求CD的值,进而可求点D和E的坐标;利用待定系数可得直线DE的解析式;
②先确定出k的值,再分情况计算S的表达式,并确认b的取值.
(1)∵O(0,0),A(6,0),C(0,3),
∴OA=6,OC=3,
∵四边形OABC是矩形,
∴AB=OC=3,BC=OA=6,
∴B(6,3),
∵动点F从O点以每秒1个单位长的速度沿OC向终点C运动,运动![]() 秒时,动点E从点A出发以相等的速度沿AO向终点O运动,
秒时,动点E从点A出发以相等的速度沿AO向终点O运动,
∴当点E的运动时间为t(秒)时,
AE=t,OF=![]() +t,
+t,
则OE=OA-AE=6-t,
故答案为:6-t,![]() +t;
+t;
(2)①当t=1时,OF=1+![]() =
=![]() ,OE=6-1=5,则CF=OC-OF=3-
,OE=6-1=5,则CF=OC-OF=3-![]() =
=![]() ,
,

由折叠可知:△OEF≌△DEF,
∴OF=DF=![]() ,
,
由勾股定理,得:CD=1,
∴D(1,3);
∵E(5,0),
∴设直线DE的解析式为:y=mx+n(k≠0),
把D(1,3)和E(5,0)代入得:![]() ,解得:
,解得: ,
,
∴直线DE的解析式为:y=-![]() ;
;
②∵MN∥DE,
∴MN的解析式为:y=-![]() ,
,
当y=3时,-![]() =3,x=
=3,x=![]() (b-3)=
(b-3)=![]() b-4,
b-4,
∴CM=![]() b-4,
b-4,
分三种情况:
i)当M在边CB上时,如图2,

∴BM=6-CM=6-(![]() b-4)=10-
b-4)=10-![]() b,
b,
DM=CM-1=![]() b-5,
b-5,
∵0≤DM<5,即0≤![]() b-5<5,
b-5<5,
∴![]() ≤b<
≤b<![]() ,
,
∴S=![]() BMAB=
BMAB=![]() ×3(10
×3(10![]() b)=15-2b=-2b+15(
b)=15-2b=-2b+15(![]() ≤b<
≤b<![]() );
);
ii)当M与点B重合时,b=![]() ,S=0;
,S=0;
iii)当M在DB的延长线上时,如图3,

∴BM=CM-6=![]() b-10,
b-10,
DM=CM-1=![]() b-5,
b-5,
∵DM>5,即![]() b-5>5,
b-5>5,
∴b>![]() ,
,
∴S=![]() ×3(
×3(![]() b10)=2b-15(b>
b10)=2b-15(b>![]() );
);
综上, .
.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
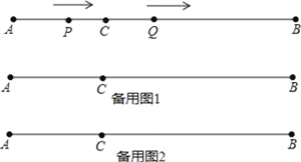
【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P、Q两点停止运动.
(1)AC=__cm,BC=__cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,PQ=1cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位为1的方格纸上,![]()
![]() ……,都是斜边在
……,都是斜边在![]() 轴上,斜边长分别为2,4,6……的等腰直角三角形,若
轴上,斜边长分别为2,4,6……的等腰直角三角形,若![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,则依图中所示规律,
,则依图中所示规律,![]() 的坐标为__________.
的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,对角线AC,BD相交于O,BD=2AD,E,F,G分别是OC,OD,AB的中点,下列结论

①BE⊥AC
②四边形BEFG是平行四边形
③EG=GF
④EA平分∠GEF
其中正确的是( )
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,且OA=OB
(1)求证:四边形ABCD是矩形;
(2)若AB=5,∠AOB=60°,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,17,4分)已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 .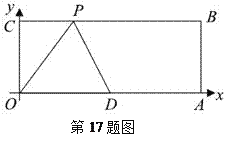
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的“探究”.
(提出问题)三个有理数a、b、c满足abc>0,求![]() 的值.
的值.
(解决问题)由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c都是正数,即a>0,b>0,c>0时,
则:![]() =
=![]() =1+1+1=3;
=1+1+1=3;
②当a,b,c有一个为正数,另两个为负数时,设a>0,b<0,c<0,
即:![]() =
=![]() =1+(1)+(1)=1,所以
=1+(1)+(1)=1,所以![]() 的值为3或1.
的值为3或1.
(探究)请根据上面的解题思路解答下面的问题:
(1)已知a<0,b>0,c>0,则![]() ,
,![]() ,
,![]() ;
;
(2)三个有理数a,b,c满足abc<0,求![]() 的值;
的值;
(3)已知|a|=3,|b|=1,且a<b,求a+b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com