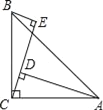
【题目】如图，∠ACB=90°，AC=BC，BE⊥CE，AD⊥CE于D，若AD的长为2x+3，BE的长为x+1，ED=5，则x的值为_____．
【答案】3
【解析】解：∵BE⊥CE，AD⊥CE，
∴∠BCE+∠ACD=90°，∠CAD+∠ACD=90°，
∴∠BCE=∠CAD，
在△BCE与△CAD中
∵AC=BC,
∠BEC=∠CDA,
∠BCE=∠ACD,，
∴△BCE≌△CAD，
∴BE=CD，AD=CE，
又∵AD的长为2x+3，BE的长为x+1，ED=5，
∴CD+DE=CE=AD，即可得出方程x+1+5=2x+3，
解得：x=3．
点睛:首先判断出∠BCE=∠ACD，再结合AC=BC，∠BEC=∠CDA=90°，可判断△BCE≌△CAD，得出BE=CD，AD=CE，从而根据CD+DE=CE=AD，得出方程x+1+5=2x+3，解出即可得出x的值．
科目：初中数学 来源： 题型：
【题目】(1)已知图1将线段AB向右平移1个单位长度,图2是将线段AB折一下再向右平移1个单位长度,请在图3中画出一条有两个折点的折线向右平移1个单位长度的图形；
(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩下部分的面积；
(3)如图4，在宽为10 m,长为40 m的长方形菜地上有一条弯曲的小路,小路宽度为1 m,求这块菜地的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，在△ABC中，∠BAC=90°，AB=AC，AO⊥BC于点O，点F是线段AO上的点(与A，O不重合)，∠EAF=90°，AE=AF，连接FE，FC，BE，BF.
(1)求证：BE=BF；
(2)如图②，若将△AEF绕点A旋转，使边AF在∠BAC的内部，延长CF交AB于点G，交BE于点K.求证：△AGC∽△KGB.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在下列条件中，不能作为判断△ABD≌△BAC的条件是（ )
A. ∠D＝∠C，∠BAD＝∠ABC B. ∠BAD＝∠ABC，∠ABD＝∠BAC
C. BD＝AC，∠BAD＝∠ABC D. AD＝BC，BD＝AC
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AD⊥BC于点D，BE平分∠ABC，若∠ABC=64°，∠AEB=70°．
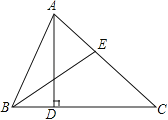
（1）求∠CAD的度数；
（2）若点F为线段BC上的任意一点，当△EFC为直角三角形时，求∠BEF的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】探究应用：用“∪”、“∩”定义两种新运算：对于两数a、b，规定a∪b＝10a×10b，a∩b＝10a÷10b，例如：3∪2＝103×102＝105，3∩2＝103÷102＝10．
(1) 求: (2017∪983) 的值
(2) 求: (2018∩2016) 的值；
(3) 当x为何值时， (x∪5)的值与 (23∩17)的值相等．
查看答案和解析>>
科目：初中数学 来源： 题型：
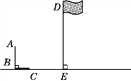
【题目】如图，九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度，已知直立在地面上的竹竿AB的长为3 m．某一时刻，测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影，并写出画图步骤；
(2)在测量竹竿AB的影长时，同时测得旗杆DE在阳光下的影长为6 m，请你计算旗杆DE的高度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD和四边形
位似，位似比
=2，四边形A′B′C′D′和四边形
位似，位似比
=1．四边形
和四边形ABCD是位似图形吗？位似比是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
