
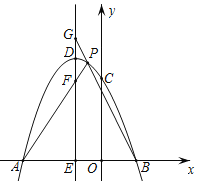
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点(A在B的左侧),且OA=3,OB=1,与y轴交于C(0,3),抛物线的顶点坐标为D(﹣1,4).
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)过点D作直线DE∥y轴,交x轴于点E,点P是抛物线上B、D两点间的一个动点(点P不与B、D两点重合),PA、PB与直线DE分别交于点F、G,当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.
【答案】(1)A点坐标(﹣3,0),B点坐标(1,0);(2)抛物线的解析式为y=﹣x2﹣2x+3;(3)EF+EG=8(或EF+EG是定值),理由见解析.
【解析】(1)根据OA,OB的长,可得答案;
(2)根据待定系数法,可得函数解析式;
(3)根据相似三角形的判定与性质,可得EG,EF的长,根据整式的加减,可得答案.
(1)由抛物线y=ax2+bx+c交x轴于A、B两点(A在B的左侧),且OA=3,OB=1,得
A点坐标(﹣3,0),B点坐标(1,0);
(2)设抛物线的解析式为y=a(x+3)(x﹣1),
把C点坐标代入函数解析式,得
a(0+3)(0﹣1)=3,
解得a=﹣1,
抛物线的解析式为y=﹣(x+3)(x﹣1)=﹣x2﹣2x+3;
(3)EF+EG=8(或EF+EG是定值),理由如下:
过点P作PQ∥y轴交x轴于Q,如图,
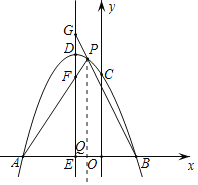
设P(t,﹣t2﹣2t+3),
则PQ=﹣t2﹣2t+3,AQ=3+t,QB=1﹣t,
∵PQ∥EF,
∴△AEF∽△AQP,
∴![]() ,
,
∴EF=![]() =
=![]() ;
;
又∵PQ∥EG,
∴△BEG∽△BQP,
∴![]() ,
,
∴EG=![]() =
=![]() =2(t+3),
=2(t+3),
∴EF+EG=2(1﹣t)+2(t+3)=8.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为 ,线段AD、BE之间的关系 .
(2)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.①请判断∠AEB的度数,并说明理由;②当CM=5时,AC比BE的长度多6时,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
(1)如图1,点E,F在AB,AC上,且∠EDF=90°.求证:BE=AF;
(2)点M,N分别在直线AD,AC上,且∠BMN=90°.
①如图2,当点M在AD的延长线上时,求证:AB+AN=![]() AM;
AM;
②当点M在点A,D之间,且∠AMN=30°时,已知AB=2,直接写出线段AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车经销商计划投入7.1万元购进100辆A型和30辆B型自行车,其中B型车单价是A型车单价的6倍少60元.
(1)求A、B两种型号的自行车单价分别是多少元?
(2)后来由于该经销商资金紧张,投入购车的资金不超过5.86万元,但购进这批自行年的总数不变,那么至多能购进B型车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
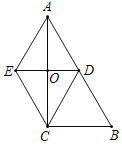
【题目】如图,在△ABC中,∠ACB=90°,O、D分别是边AC、AB的中点,过点C作CE∥AB交DO的延长线于点E,连接AE.
(1)求证:四边形AECD是菱形;
(2)若四边形AECD的面积为24,tan∠BAC=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C为数轴上的三点,动点A、B同时从原点出发,动点A每秒运动x个单位,动点B每秒运动y个单位,且动点A运动到的位置对应的数记为a,动点B运动到的位置对应的数记为b,定点C对应的数为8.
(1)若2秒后,a、b满足|a+8|+|b﹣2|=0,则x= ,y= .并请在数轴上标出A、B两点的位置.
(2)若动点A、B在(1)运动后的位置上保持原来的速度,且同时向正方向运动z秒后使得|a|=|b|,使得z= .
(3)若动点A、B在(1)运动后的位置上都以每秒2个单位向正方向运动继续运动t秒,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,点A与点B之间的距离为AB,且AC+BC=1.5AB,则t= .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图点 P 是等边△ABC 内一点,将△APC 绕点 C 顺时针旋转 60°得到△BDC,连接 PD.
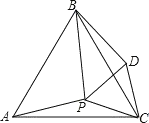
(1)求证:△DPC 是等边三角形;
(2)当∠APC=150°时,试判断△DPB 的形状,并说明理由;
(3)当∠APB=100°且△DPB 是等腰三角形,求∠APC 的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
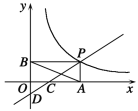
【题目】如图,直线![]() 与x轴、y轴分别交于C、D两点,与双曲线
与x轴、y轴分别交于C、D两点,与双曲线![]() 在第一象限内交于点P,过点P作PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,4)且S△DBP=27.
在第一象限内交于点P,过点P作PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,4)且S△DBP=27.
(1)直接写出直线的解析式_____________,双曲线的解析式____________;
(2)设点Q是直线![]() 上的一点,且满足△DOQ的面积是△COD面积的2倍,请求出点Q的坐标;
上的一点,且满足△DOQ的面积是△COD面积的2倍,请求出点Q的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | 22.8 |
八(2) | a | 85 | 85 | 19.2 |
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com