
����Ŀ��A��B��CΪ�����ϵ����㣬����A��Bͬʱ��ԭ�����������Aÿ���˶�x����λ������Bÿ���˶�y����λ���Ҷ���A�˶�����λ�ö�Ӧ������Ϊa������B�˶�����λ�ö�Ӧ������Ϊb������C��Ӧ����Ϊ8��
��1����2���a��b����|a+8|+|b��2|��0����x���� ����y���� ���������������ϱ��A��B�����λ�ã�
��2��������A��B�ڣ�1���˶����λ���ϱ���ԭ�����ٶȣ���ͬʱ���������˶�z���ʹ��|a|��|b|��ʹ��z���� ����
��3��������A��B�ڣ�1���˶����λ���϶���ÿ��2����λ���������˶������˶�t�룬��A���C֮��ľ����ʾΪAC����B���C֮��ľ����ʾΪBC����A���B֮��ľ���ΪAB����AC+BC��1.5AB����t���� ����
![]()
���𰸡���1��4��1��ͼ�����������2��![]() ��
��![]() ����3��
����3��![]() ��
��![]() ��
��
��������
��1����|a+8|+��b��2��2=0��
��a+8=0��b��2=0����a=��8��b=2��
��x=|��8|��2=4��y=2��2=1��
�������ϱ��A��B�����λ������ͼ��ʾ��
![]()
�ʴ�Ϊ��4��1��
��2���߶���A��B�ڣ�1���˶����λ���ϱ���ԭ�����ٶȣ���ͬʱ���������˶�z���
��a=��8+4z��b=2+z��
��|a|=|b|��
��|��8+4z|=|2+z|��
�ੁ8+4z+2+z=0��8+4z=2+z
��ã�z=![]() ��z=
��z=![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��3��������A��B�ڣ�1���˶����λ���϶���ÿ��2����λ���������˶������˶�t���
���A��ʾ����8+2t����B��ʾ��2+2t����C��ʾ��8��
��AC=|��8+2t��8|=|2t��16|��BC=|2+2t��8|=|2t��6|��AB=|��8+2t����2+2t��|=10��
��AC+BC=1.5AB��
��|2t��16|+|2t��6|=1.5��10��
������������ۣ�
�ٵ�t��3ʱ��
16-2t+6-2t=15��
��ã�t=![]() ��
��
�ڵ�3��t��8ʱ��
16-2t+2t-6=10��15
�����⣻
�۵�t��8ʱ��
2t-16+2t-6=15
��ã�t=![]() ��
��
����������t=![]() ��t=
��t=![]() ��
��
�ʴ�Ϊ��![]() ��
�� ![]() ��
��


 ��ҵ����ϵ�д�
��ҵ����ϵ�д� ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽���뷢�֣�
��ͼ1��ʾ��ͼ�Σ������dz�����ѧϰ��Ʒ����Բ�森���Dz���������ͼ�ν���������ͼ������ô����һ����ͼ���У�������������Щ��ѧ֪ʶ�أ���������㷢����Ĵ������ǣ�����������⣺
��1���۲�������ͼ������̽����BDC���A����B����C֮��Ĺ�ϵ����˵�����ɣ�
��2������ֱ���������Ͻ��ۣ���������������⣺
����ͼ2����һ�����dz�XYZ��������ABC�ϣ�ʹ���dzߵ�����ֱ�DZ�XY��XZǡ�þ�����B��C������A=50�������ABX+��ACX=__________�㣻
����ͼ3��DCƽ�֡�ADB��ECƽ�֡�AEB������DAE=50�㣬��DBE=130�������DCE�Ķ�����
����ͼ4����ABD����ACD��10�ȷ����ཻ�ڵ�G1��G2����G9������BDC=140�㣬��BG1C=77�������A�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м��� 27a8 ![]() a3 9a 2 ��˳����ȷ���ǣ� ��
a3 9a 2 ��˳����ȷ���ǣ� ��
A.(27 ![]() 9)a83 2B.(27a8
9)a83 2B.(27a8 ![]() a3 ) 9a 2
a3 ) 9a 2
C.27a8 (![]() a3 9a 2 )D.(27a8 9a 2 )
a3 9a 2 )D.(27a8 9a 2 ) ![]() a3
a3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
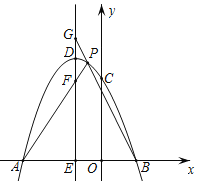
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c��x����A��B���㣨A��B����ࣩ����OA=3��OB=1����y�ύ��C��0��3���������ߵĶ�������ΪD����1��4����
��1����A��B��������ꣻ
��2���������ߵĽ���ʽ��
��3������D��ֱ��DE��y�ᣬ��x���ڵ�E����P����������B��D������һ�����㣨��P����B��D�����غϣ���PA��PB��ֱ��DE�ֱ��ڵ�F��G������P�˶�ʱ��EF+EG�Ƿ�Ϊ��ֵ�����ǣ�������ö�ֵ�������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��BAE����AED��180������1����2����ô��F����G��Ϊʲô��
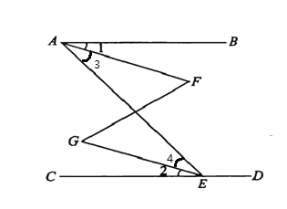
�⣺��Ϊ��BAE����AED��180��( ��֪)
����AB��CD________
���ԡ�BAE����AEC________
��Ϊ��1����2( ��֪)
���ԡ�BAE����1����AEC����2(��ʽ����)
����3����4
����AF��EG________��
���ԡ�F����G________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2014����ǭ����)ǭ������ij���мƻ�����һ���ס���������ߣ���֪5��������ߵĽ�����3��������ߵĽ��۵ĺ�Ϊ231Ԫ��2��������ߵĽ�����3��������ߵĽ��۵ĺ�Ϊ141Ԫ��
(1)��ÿ�����֡�������ߵĽ��۷ֱ��Ƕ���Ԫ��
(2)�����������������Żݣ��Żݷ����ǣ�����������߳���20�����������ֿ�������7���Żݣ�������x(x��0)�����������Ҫ����yԪ���������y��x�ĺ�����ϵʽ��
(3)��(2)�������£����о����ڼס������������ѡ������һ�֣�����������20����������������жϹ����������ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
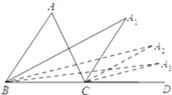
����Ŀ����ͼ��BA1��CA1�ֱ��ǡ�ABC���ڽ�ƽ���ߺ����ƽ���ߣ� BA2�ǡ�A1BD�Ľ�ƽ���ߣ�CA2 �ǡ�A1CD�Ľ�ƽ���ߣ�BA3�ǡ�A2BD�Ľ�ƽ���ߣ�CA3 �ǡ�A2CD�Ľ�ƽ���ߣ�����A�� �������A2019��______________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽������y=x+![]() ��x��0����y=x+
��x��0����y=x+![]() ��x��0��a��0����������ʣ�
��x��0��a��0����������ʣ�
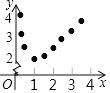
��1��С��ͬѧ�Ժ���y=x+![]() ��x��0�������������б�����㣬�������������ߵIJ��裻�۲�ͼ��ɵ�������СֵΪ�� ����������һ������Ϊ�� ����
��x��0�������������б�����㣬�������������ߵIJ��裻�۲�ͼ��ɵ�������СֵΪ�� ����������һ������Ϊ�� ����
x | �� |
|
|
| 1 |
| 2 |
| 3 | �� |
y | �� |
|
|
| 2 |
|
|
|
| �� |
��2�������䷽������y=x+![]() ��x��0������Сֵ��
��x��0������Сֵ��
��3�����뺯��y=x+![]() ��x��0��a��0������СֵΪ�� ����
��x��0��a��0������СֵΪ�� ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com