
【题目】探究函数y=x+![]() (x>0)与y=x+
(x>0)与y=x+![]() (x>0,a>0)的相关性质.
(x>0,a>0)的相关性质.
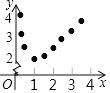
(1)小聪同学对函数y=x+![]() (x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
(x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
x | … |
|
|
| 1 |
| 2 |
| 3 | … |
y | … |
|
|
| 2 |
|
|
|
| … |
(2)请用配方法求函数y=x+![]() (x>0)的最小值;
(x>0)的最小值;
(3)猜想函数y=x+![]() (x>0,a>0)的最小值为 .
(x>0,a>0)的最小值为 .
【答案】(1)2;当x>1时,y随x的增大而增大;(2)最小值是2;(3)2![]() .
.
【解析】
(1)根据函数图象可以得到函数y=x+![]() (x>0)的最小值,然后根据函数图象,可以写出该函数的一条性质,注意函数的性质不唯一,写的只要复合函数即可;
(x>0)的最小值,然后根据函数图象,可以写出该函数的一条性质,注意函数的性质不唯一,写的只要复合函数即可;
(2)根据配方法可以求得函数y=x+![]() (x>0)的最小值;
(x>0)的最小值;
(3)根据配方法可以求得函数y=x+![]() (x>0,a>0)的最小值.
(x>0,a>0)的最小值.
(1)由图象可得,
函数y=x+![]() (x>0)的最小值是2,它的另一条性质是:当x>1时,y随x的增大而增大,
(x>0)的最小值是2,它的另一条性质是:当x>1时,y随x的增大而增大,
故答案为:2,当x>1时,y随x的增大而增大;
(2)∵y=x+![]() (x>0),
(x>0),
∴y=![]() +2,
+2,
∴当![]() 时,y取得最小值,此时x=1,y=2,
时,y取得最小值,此时x=1,y=2,
即函数y=x+![]() (x>0)的最小值是2;
(x>0)的最小值是2;
(3)∵y=x+![]() (x>0,a>0)
(x>0,a>0)
∴y=![]() +2
+2![]() ,
,
∴当![]() 时,y取得最小值,此时y=2
时,y取得最小值,此时y=2![]() ,
,
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
【题目】A、B、C为数轴上的三点,动点A、B同时从原点出发,动点A每秒运动x个单位,动点B每秒运动y个单位,且动点A运动到的位置对应的数记为a,动点B运动到的位置对应的数记为b,定点C对应的数为8.
(1)若2秒后,a、b满足|a+8|+|b﹣2|=0,则x= ,y= .并请在数轴上标出A、B两点的位置.
(2)若动点A、B在(1)运动后的位置上保持原来的速度,且同时向正方向运动z秒后使得|a|=|b|,使得z= .
(3)若动点A、B在(1)运动后的位置上都以每秒2个单位向正方向运动继续运动t秒,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,点A与点B之间的距离为AB,且AC+BC=1.5AB,则t= .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它们的面积,可以得到一个数学等式,例如图1可以得到
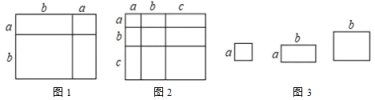
(1)类似图1的数学等式,写出图2表示的数学等式;
(2)若![]() ,
, ![]() ,用上面得到的数学等式乘
,用上面得到的数学等式乘![]() 的值;
的值;
(3)小明同学用图3中的![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张边长为
张边长为![]() 的正方形,z张边长为
的正方形,z张边长为![]() 、
、![]() 的长方形拼出一个面积为
的长方形拼出一个面积为![]() 的长方形,求
的长方形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | 22.8 |
八(2) | a | 85 | 85 | 19.2 |
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
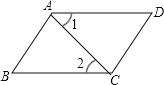
【题目】 根据题意,完成推理填空:如图,AB∥CD,∠1=∠2,试说明∠B=∠D.
解:∵∠1=∠2(已知)
∴ (內错角相等,两直线平行)
∴∠BAD+∠B=180°(两直线平行,同旁内角互补)
∵AB∥CD
∴ + =180°,
∴∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC的斜边AB=6 cm,直角边AC=3 cm.
(1)以C为圆心,2 cm长为半径的圆和AB的位置关系是_________;
(2)以C为圆心,4 cm长为半径的圆和AB的位置关系是_________;
(3)如果以C为圆心的圆和AB相切,则半径长为_________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com