
【题目】如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.

【答案】(1) ![]() ;(2)
;(2) ![]() ≤m<4
≤m<4![]() .
.
【解析】
试题分析:(1)只要证明△ABD∽△DPC,可得![]() ,由此求出PD即可解决问题;
,由此求出PD即可解决问题;
(2)分两种情形求出AD的值即可解决问题:①如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.②如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3
试题解析:(1)如图1中,
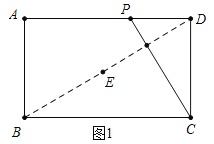
∵四边形ABCD是矩形,
∴∠ADC=∠A=90°,
∴∠DCP+∠CPD=90°,
∵∠CPD+∠ADB=90°,
∴∠ADB=∠PCD,
∵∠A=∠CDP=90°,
∴△ABD∽△DPC,
∴![]() ,
,
∴![]() ,
,
∴PD=![]() ,
,
∴t=![]() s时,B、E、D共线.
s时,B、E、D共线.
(2)如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.
作EQ⊥BC于Q,EM⊥DC于M.则EQ=3,CE=DC=4
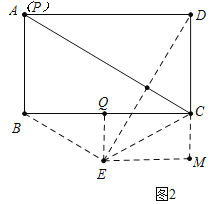
易证四边形EMCQ是矩形,
∴CM=EQ=3,∠M=90°,
∴EM=![]() ,
,
∵∠DAC=∠EDM,∠ADC=∠M,
∴△ADC∽△DME,
![]() ,
,
∴![]() ,
,
∴AD=4![]() ,
,
如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3.
作EQ⊥BC于Q,延长QE交AD于M.则EQ=3,CE=DC=4
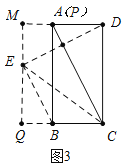
在Rt△ECQ中,QC=DM=![]() ,
,
由△DME∽△CDA,
∴![]() ,
,
∴![]() ,
,
∴AD=![]() ,
,
综上所述,在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,这样的m的取值范围![]() ≤m<4
≤m<4![]() .
.


科目:初中数学 来源: 题型:
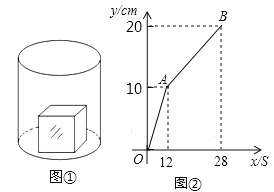
【题目】如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
(1)正方体的棱长为 cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,BO,CO分别是∠ABC和∠ACB的平分线,过O点的直线分别交AB、AC于点D、E,且DE∥BC.若AB=6cm,AC=8cm,则△ADE的周长为 . 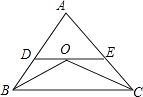
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国人很早就开始使用负数,曾在一部中国古代数学著作中首次正式引入负数及其加减法运算法则,并给出名为“正负术”的算法,这部著作采用按类分章的问题集的形式进行编排,它的出现标志着我国古代数学体系的正式确立.这部经典名著是( )
A.《海岛算经》B.《九章算术》
C.《孙子算经》D.《周髀算经》
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒的直径大约为0.00000008 m —0.00000012 m,0.00000012用科学记数法表示为( )
A.1.2×107B.12×10﹣6C.1.2×10﹣7D.0.12×10﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2014年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com