
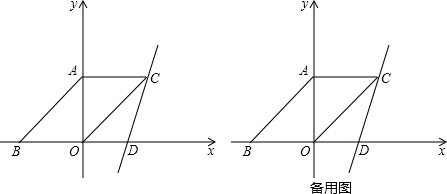
���� ��1����ƽ���ı��ε����������C�����꣬��C���������y=3x+b�������ֱ��CD�Ľ���ʽ���Ӷ����D�����ꣻ
��2�����ֱ��ED��OC�Ľ���M���ɵõ�MΪ����ֱ��������OAC���е㣬����AM�����AB��AM�ij���ͨ����BAE�ס�EAM�����AE�ij���������õ�E�����꣬�����ֱ��EC�Ľ���ʽ��
��3���������������P��OF���˶������������HEA=��GEC��Ҫʹ��EHA���EGC���ƣ�ֻҪ��HAE=��GCE=45�㼴�ɣ�����HAE=45��ʱ���С�OAP=��HAE=45�㣬�õ���AOPΪ����ֱ�������Σ��Ӷ����t��ֵ��
��P��EF���˶������������HEA=��GEC��Ҫʹ��EHA���EGC���ƣ�ֻҪ��AHE=��GCE=45�㼴�ɣ�����AHE=45��ʱ���ɡ�HEI=45�㣬�õ���HIE=90�㣬��AP��ED�����ֱ��AP�Ľ���ʽ�������ֱ��AP��EF�ý���P�����꣬�������ľ��빫ʽ���EP�ij����Ӷ��ó�PF�ij����ֱ����P��OF���˶���ʱ����P��FE���˶���ʱ�䣬������ӣ��õ�t��ֵ��
��� �⣺��1����B��-6��0����
��OB=6��
��AO=BO��
��AO=6��
���ı���ABCD��ƽ���ı���ABOC��
��AC=BO=6��
��C��6��6����
��ֱ�߹�y=3x+b��C��
��6=3��6+b
��b=-12��
��ֱ��CD�Ľ���ʽΪ��y=3x-12����y=3x-12�У���y=0��
��ã�x=4��
��D��4��0����
��2����E��0��t����t��0����EO=t��
�ߡ�BEO+��OED=45�㣬
��tan��BEO=$\frac{BO}{t}$=$\frac{6}{t}$��tan��OED=$\frac{OD}{t}=\frac{4}{t}$��
��tan����BEO+��OED��=tan45��=1=$\frac{tan��BEO+tan��OED}{1-tan��BEO•tan��OED}=\frac{10t}{{t}^{2}-24}$��
��t=12��t=-2���ᣩ��
��E��0��12����
��C��6��6����
��ֱ��EC�Ľ���ʽΪ��y=-x+12��
��3��������������ٵ�P��OF���˶�ʱ��
��ֱ��EC�Ľ���ʽΪ��y=-x+12����y=0���ã�x=12��
��OF=OE=12�����OFE=45�㣬
��AC��OB��
���ACE=��OFE=45�㣬
���CEG+��AEG=45�㣬
�ߡ�BAD=45�㣬
���HEA=��GEC��
Ҫʹ��EHA���EGC���ƣ�ֻҪ��HAE=��GCE=45�㼴�ɣ�����HAE=45��ʱ����OAP=��HAE=45�㣬
���AOPΪ����ֱ�������Σ�
��OP=OA=6��
��t=6��2=3��
�ڵ�P��EF���˶�ʱ���ɢٿ�֪����EHA���EGC�У���HEA=��GEC����GCE=45�㣬
��ֻ��Ҫ��EHA=45�㼴�ɣ�����EHA=45��ʱ��
�ߡ�HEI=45�㣬
���HIE=90�㣬
��AP��ED��
��ֱ��AP�Ľ���ʽΪ��y=$\frac{1}{3}$x+n��
��A��0��6�����룬�ã�n=6��
��ֱ��AP�Ľ���ʽΪ��y=$\frac{1}{3}$x+6��
�������̣�$\left\{\begin{array}{l}{y=\frac{1}{3}x+6}\\{y=-x+12}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=4.5}\\{y=7.5}\end{array}\right.$��
��P��4.5��7.5����
��EP=$\frac{9\sqrt{2}}{2}$��
��EF=$\sqrt{2}$OE=12$\sqrt{2}$��
��FP=12$\sqrt{2}$-$\frac{9\sqrt{2}}{2}$=$\frac{15\sqrt{2}}{2}$��
���P��O��P���õ�ʱ��=12��2+$\frac{15\sqrt{2}}{2}$��$\sqrt{2}$=$\frac{27}{2}$��
���� ���⿼�����������ۺ��⣬�õ���֪ʶ�������������ε��жϺ����ʡ�ƽ���ı��ε����ʡ����ô���ϵ������һ�κ����Ľ���ʽ������ֱ�������ε��жϺ����ʣ���Ŀ���ۺ��Խ�ǿ�ѶȽϴ�ѧ���Ľ���������ǿ�ܸߣ�����Ĺؼ������÷������۵���ѧ˼�룬��ȡ�������ⲹ�䲻©��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
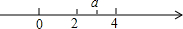 ʵ��a�������ϵ�λ����ͼ��ʾ������|a-2|+$\sqrt{{a}^{2}-8a+16}$=2��
ʵ��a�������ϵ�λ����ͼ��ʾ������|a-2|+$\sqrt{{a}^{2}-8a+16}$=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD��AE�۵���ʹ��D����BC���ϵ�F�㴦��AD=5��AB=4����CE�ij���
��ͼ������ABCD��AE�۵���ʹ��D����BC���ϵ�F�㴦��AD=5��AB=4����CE�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����Ա߷ֱ�ƽ�е��ı��ν���ƽ���ı��� | |
| B�� | ��������������ĵ��������� | |
| C�� | ��ͬһƽ���������߶���β˳�����ӵõ���ͼ�ν��������� | |
| D�� | ����δ֪���ĵ�ʽ�������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com