
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 于点H,点D在AH上,且
于点H,点D在AH上,且![]() ,连接BD.
,连接BD.
![]() 如图1,将
如图1,将![]() 绕点H旋转,得到
绕点H旋转,得到![]() 点B、D分别与点E、F对应
点B、D分别与点E、F对应![]() ,连接AE,当点F落在AC上时
,连接AE,当点F落在AC上时![]() 不与C重合
不与C重合![]() ,求AE的长;
,求AE的长;
![]() 如图2,
如图2,![]() 是由
是由![]() 绕点H逆时针旋转
绕点H逆时针旋转![]() 得到的,射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由.
得到的,射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由.

【答案】(1)证明见解析;(2)(I)AE=![]() ;(II)
;(II)![]() .
.
【解析】
(1)先根据tanC=3,求出AH=3,CH=1,然后根据△EHA∽△FHC,得到,HP=3AP,AE=2AP,最后用勾股定理即可;
(2)先判断出△AGQ∽△CHQ,得到![]() ,然后判断出△AQC∽△GQH,用相似比即可.
,然后判断出△AQC∽△GQH,用相似比即可.
(1)如图,
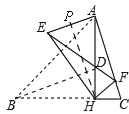
在Rt△AHC中,
∵tanC=3,
∴![]() =3,
=3,
设CH=x,
∴BH=AH=3x,
∵BC=4,
∴3x+x=4,
∴x=1,
∴AH=3,CH=1,
由旋转知,∠EHF=∠BHD=∠AHC=90°,EH=AH=3,CH=DH=FH,
∴∠EHF+∠AHF=∠AHC+∠AHF,
∴∠EHA=∠FHC,![]() =1,
=1,
∴△EHA∽△FHC,
∴∠EAH=∠C,
∴tan∠EAH=tanC=3,
过点H作HP⊥AE,
∴HP=3AP,AE=2AP,
在Rt△AHP中,AP2+HP2=AH2,
∴AP2+(3AP)2=9,
∴AP=![]() ,
,
∴AE=![]() ;
;
(2)如图1,
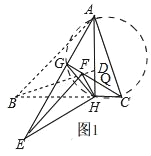
∵△EHF是由△BHD绕点H逆时针旋转30°得到,
∴HD=HF,∠AHF=30°
∴∠CHF=90°+30°=120°,
由(1)有,△AEH和△FHC都为等腰三角形,
∴∠GAH=∠HCG=30°,
∴CG⊥AE,
∴点C,H,G,A四点共圆,
∴∠CGH=∠CAH,
设CG与AH交于点Q,
∵∠AQC=∠GQH,
∴△AQC∽△GQH,
∴![]() ,
,
∵△EHF是由△BHD绕点H逆时针旋转30°得到,
∴EF=BD,
由(1)知,BD=AC,
∴EF=AC
∴![]() =2,
=2,
即:EF=2HG,


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
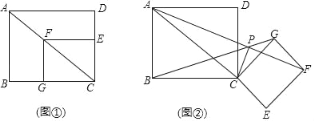
【题目】如图①,四边形ABCD与四边形CEFG都是矩形,点E,G分别在边CD,CB上,点F在AC上,AB=3,BC=4
(1)求![]() 的值;
的值;
(2)把矩形CEFG绕点C顺时针旋转到图②的位置,P为AF,BG的交点,连接CP
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)判断CP与AF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
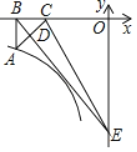
【题目】如图点A在反比例函数y=![]() (x<0)的图象上,作Rt△ABC,直角边BC在x轴上,点D为斜边AC的中点,直线BD交y轴于点E,若△BCE的面积为8,则k=_____.
(x<0)的图象上,作Rt△ABC,直角边BC在x轴上,点D为斜边AC的中点,直线BD交y轴于点E,若△BCE的面积为8,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(![]() ,
,![]() ),点Q的坐标为(
),点Q的坐标为(![]() ,
,![]() ),且
),且![]() ,
,![]() ,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
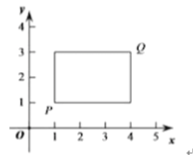
(1)已知点A的坐标为(1,0).
①若点B的坐标为(3,1)求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)⊙O的半径为![]() ,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图,在一滑梯侧面示意图中,BD∥AF,BC⊥AF于点C,DE⊥AF于
点E.BC=1.8m,BD=0.5m,∠A=45,∠F=29.
(1)求滑道DF的长(精确到0.1m);
(2)求踏梯AB底端A与滑道DF底端F的距离AF(精确到0.1m).
(参考数据:sin29≈0.48,cos29≈0.87,tan29≈0.55)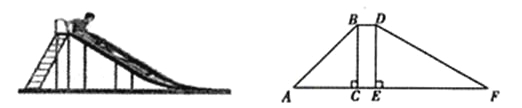
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠B=60°,对角线AC平分角∠BAD,点P是△ABC内一点,连接PA、PB、PC,若PA=6,PB=8,PC=10,则菱形ABCD的面积等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小山的东侧A点有一个热气球,由于受风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A,B两点间的距离为( )米.
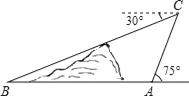
A. 750![]() B. 375
B. 375![]() C. 375
C. 375![]() D. 750
D. 750![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com