
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=
 的图象上,过点A的直线y=x+b交反比例函数y=
的图象上,过点A的直线y=x+b交反比例函数y=
 的图象于另一点B.
的图象于另一点B.
(1)求k和b的值;
(2)求△OAB的面积.


【考点】反比例函数与一次函数的交点问题.
【专题】计算题.
【分析】(1)只需把点A的坐标代入一次函数和反比例函数的解析式,就可解决问题;
(2)只需求出直线AB与y轴的交点,然后运用割补法就可解决问题.
【解答】解:(1)∵点A(2,5)是直线y=x+b与反比例函数y=
 的图象的一个交点,
的图象的一个交点,
∴5=2+b,k=2×5=10,
∴b=3,
即k和b的值分别为10、3;
(2)解方程组
 ,得
,得
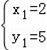
 ,
,

∴点B(﹣5,﹣2).
∵点C是直线y=x+3与y轴的交点,
∴点C(0,3),
∴S△OAB=S△OAC+S△OBC
=
 ×3×2+
×3×2+
 ×3×5=
×3×5=
 ,
,
即△OAB的面积为
 .
.


【点评】本题主要考查了直线与反比例函数图象上点的坐标特征、运用待定系数法求直线与反比例函数的解析式、解方程组等知识,运用割补法是解决第(2)小题的关键.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
如图,已知四边形ABCD是边长为2的正方形,以对角线BD为边作正三角形BDE,过E作DA的延长线的垂线EF,垂足为F.
(1)找出图中与EF相等的线段,并证明你的结论;
(2)求AF的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图1所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20cm,且AH=DE=EG=20cm.
(1)当∠CED=60°时,CD= .
(2)当∠CED由60°变为120°时,点A向左移动了 cm(结果精确到0.1cm)(参考数据
 ≈1.73).
≈1.73).


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com