Question

如图1所示的晾衣架，支架主视图的基本图形是菱形，其示意图如图2，晾衣架伸缩时，点G在射线DP上滑动，∠CED的大小也随之发生变化，已知每个菱形边长均等于20cm，且AH=DE=EG=20cm．

（1）当∠CED=60°时，CD=　 　．

（2）当∠CED由60°变为120°时，点A向左移动了　 　cm（结果精确到0.1cm）（参考数据≈1.73）．

Answer 1

【考点】解直角三角形的应用．

【分析】（1）连接CD，由已知条件中CE=DE，∠CED=60°可知△CED为等边三角形，从而得出CD的长度；

（2）由图可知AD=3CD，由（1）可得知∠CED=60°时AD的长度；当∠CED=120°时，过点E作EH⊥CD于H，在Rt△CEH中用特殊角的三角函数值可求出CH的长度，从而得出CD和AD的长度．

【解答】解：（1）连接CD，如图1所示．

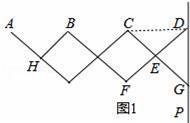
∵CE=DE=20cm，∠CED=60°，

∴△CED是等边三角形，

∴CD=DE=20cm．

故答案为：20cm．

（2）过点E作EH⊥CD于点H，如图2所示．

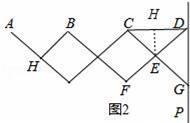
根据题意得：AB=BC=CD，

当∠CED=60°时，AD=3CD=60cm；

当∠CED=120°时，∠CEH=60°，CH=HD，

在Rt△CEH中，sin∠CEH=，

∴CH=20sin60°=20×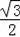=10（cm），

∴CD=20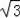（cm），

∴AD=3×2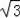0=60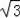≈103.8（cm），

∴103.8﹣60=43.8（cm），即点A向左移动了43.8cm．

故答案为：43.8cm．

【点评】本题考查了等边三角形的判定及性质、解直角三角形以及特殊角的三角函数值，解题的关键：（1）找出△CED为等边三角形；（2）在Rt△CEH中利用特殊角的三角函数值求边的长度．本题属于中档题，难度不大，本题与现实生活联系紧密，是数学知识应用到实际的一个很好的案例．