
如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点B,延长BO与⊙O交于点D,与PA的延长线交于点E,
(1)求证:PB为⊙O的切线;
(2)若OC:BC=2:3,求sinE的值.


【考点】切线的判定与性质.
【分析】(1)连接OA,由SSS证明△PBO≌△PAO,得出∠PBO=∠PAO=90°即可;
(2)连接AD,证明△ADE∽△POE,得到
 =
=
 ,证出OC是△ABD的中位线,由三角形中位线定理得出AD=2OC,由已知设OC=2t,则BC=3t,AD=4t.由△PBC∽△BOC,可求出sin∠E的值.
,证出OC是△ABD的中位线,由三角形中位线定理得出AD=2OC,由已知设OC=2t,则BC=3t,AD=4t.由△PBC∽△BOC,可求出sin∠E的值.
【解答】(1)证明:连接OA,如图1所示:
∵PA为⊙O的切线,
∴∠PAO=90°,
∵OA=OB,OP⊥AB于C,
∴BC=CA,PB=PA,
在△PBO和△PAO中,
 ,
,
∴△PBO≌△PAO(SSS),
∴∠PBO=∠PAO=90°,
∴PB为⊙O的切线;
(2)解:连接AD,如图2所示:
∵BD是直径,∠BAD=90°
由(1)知∠BCO=90°
∴AD∥OP,
∴△ADE∽△POE,
∴
 =
=
 ,
,
∵BC=AC,OB=OD,
∴OC是△ABD的中位线,
∴AD=2OC,
∵OC:BC=2:3,
设OC=2t,则BC=3t,AD=4t.
∵∠OBC+∠PBC=90°,∠BOC+∠OBC=90°,
∴∠BOC=∠PBC,
∵∠OCB=∠BCP,
∴△PBC∽△BOC,
∴
 ,即
,即
 ,
,
∴PC=
 t,OP=
t,OP=
 t.
t.
∴
 =
=
 =
=
 ,
,
设EA=8m,EP=13m,则PA=5m.
∵PA=PB,
∴PB=5m,
∴sinE=
 =
=
 .
.




【点评】本题考查了切线的判定与性质、全等三角形的判定与性质、相似三角形的判定和性质、三角形中位线定理等知识;熟练掌握切线的判定,能够通过作辅助线将所求的角转移到相应的直角三角形中是解答问题(2)的关键.


科目:初中数学 来源: 题型:
如图1所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20cm,且AH=DE=EG=20cm.
(1)当∠CED=60°时,CD= .
(2)当∠CED由60°变为120°时,点A向左移动了 cm(结果精确到0.1cm)(参考数据
 ≈1.73).
≈1.73).


查看答案和解析>>
科目:初中数学 来源: 题型:
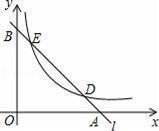
已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=
 (m≠0,x>0)分别交于D、E两点,若点D的坐标为(4,1),点E的坐标为(1,n)
(m≠0,x>0)分别交于D、E两点,若点D的坐标为(4,1),点E的坐标为(1,n)
(1)分别求出直线l与双曲线的解析式;
(2)求△EOD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
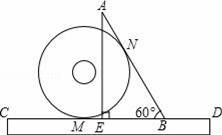
小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切时,光盘的圆心经过的距离是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com