
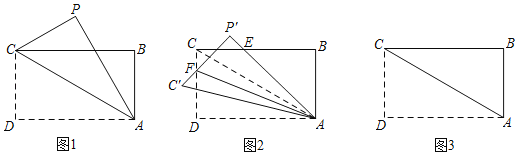
【题目】如图1,在矩形纸片ABCD中,AB=2![]() ,AD=6,将纸片沿对角线AC对折,点D落在点P处.
,AD=6,将纸片沿对角线AC对折,点D落在点P处.
(1)填空:∠BCA的大小是 ;
(2)如图2,吕家三少将折叠后的纸片沿着AC剪开,把△APC绕点A逆时针旋转α角(0°≤α≤90°),得到△AP′C′,点P,C分别对应点P′,C′,P′A交BC于点E,P′C′交CD于点F.
①点α=15时,求证:AB=BE;
②填空:当点P′落在边BC上时,连接AF,则tan∠DAF的值为 ;
③填空:在②的条件下,将△AP′C′沿着AP′折叠至△AP′C″处,点C′对应点C″,AC″交BC于点G,则线段BG的长度为 .
【答案】(1)30°;(2)①详见解析;②![]() ③
③![]()
【解析】
(1)求出∠ACB的正切值即可解决问题;
(2)①证明∠BAE=45°即可解决问题;
②利用相似三角形的性质求出CF即可解决问题;
③如图3﹣2中,作GH⊥AP′于H,设GH=x.构建方程求出x,再利用勾股定理求解即可.
(1)∵四边形ABCD是矩形,
∴∠B=90°,AD=BC=6,AB=CD=2![]() ,
,
∴tan∠ACB=![]() ,
,
∴∠ACB=30°,
故答案为:30°;
(2)①如图2﹣1中,
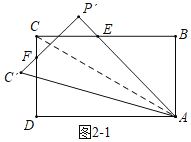
∵在Rt△ABC中,∠ACB=30°,∠B=90°,
∴∠CAB=60°,
∵α=15°,
∴∠CAE=15°,
∴∠BAE=45°,
∴∠AEB=∠EAB=45°,
∴BA=BE;
②如图2﹣2中,
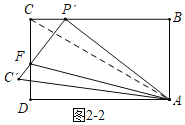
在Rt△ABP′中,BP′=![]() =2
=2![]() ,
,
∴CP′=6﹣2![]() ,
,
∵∠CFP′+∠FP′C=90°,∠FP′C+∠AP′B=90°,
∴∠AP′B=∠CFP′,
∵∠FCP′=∠B=90°,
∴△FCP′∽△P′BA,
∴![]() ,
,
∴![]() ,
,
∴CF=6![]() ﹣4
﹣4![]() ,
,
∴DF=2![]() ﹣(6
﹣(6![]() ﹣4
﹣4![]() )=6
)=6![]() ﹣6
﹣6![]() ,
,
∴tan∠DAF=![]() =
=![]() ﹣
﹣![]() ,
,
故答案为:![]() ﹣
﹣![]() ;
;
③如图2-3中,作GH⊥AP′于H,设GH=x,

由△P′HG∽△P′BA,可得P′H=![]() x,
x,
∵∠GAH=30°,∠GHA=90°,
∴AH=![]() x,
x,
∵AP′=6,
∴![]() x+
x+![]() x=6,
x=6,
∴x=6(![]() ﹣
﹣![]() ),
),
∴AG=2GH=12(![]() ﹣
﹣![]() ),
),
在Rt△ABG中,BG=![]() =8
=8![]() ﹣18,
﹣18,
故答案为:![]() ﹣18.
﹣18.


科目:初中数学 来源: 题型:
【题目】为参加11月23日举行的丹东市“我爱诗词”中小学生诗词大赛决赛,某校每班选25名同学参加预选赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为10分、9分、8分、7分,学校将八年级的一班和二班的成绩整理并绘制成如下统计图:

根据以上提供的信息解答下列问题
(1)请补全一班竞赛成绩统计图;
(2)请直接写出a、b、c、d的值;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
一班 | a= | b= | 9 |
二班 | 8.76 | c= | d= |
(3)请从平均数和中位数两个方面对这两个班级的成绩进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数y=-![]() 和y=
和y=![]() 的图象交于A点和B点.若C为x轴上任意一点,连接AC、BC,则△ABC的面积为 .
的图象交于A点和B点.若C为x轴上任意一点,连接AC、BC,则△ABC的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:h),随机调査了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
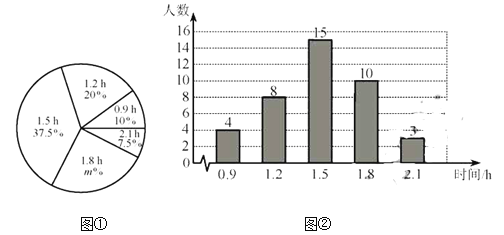
(Ⅰ)本次接受调查的初中学生人数为___________,图①中m的值为_____________;
(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有800名初中学生,估计该校每天在校体育活动时间大于1h的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
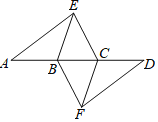
【题目】如图,点A、B、C、D依次在同一条直线上,点E、F分别在直线AD的两侧,已知BE∥CF,∠A=∠D,AE=DF.
(1)求证:四边形BFCE是平行四边形;
(2)填空:若AD=7,AB=2.5,∠EBD=60°,当四边形BFCE是菱形时,菱形BFCE的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“我为祖国点赞”征文活动中,学校计划对获得一、二等奖的学生分别奖励一支钢笔,一本笔记本.已知购买2支钢笔和3个笔记本共38元,购买4支钢笔和5个笔记本共70元.
(1)钢笔、笔记本的单价分别为多少元?
(2)经与商家协商,购买钢笔超过30支时,每增加一支,单价降低0.1元;超过50支,均按购买50支的单价销售.笔记本一律按原价销售.学校计划奖励一、二等奖学生共计100人,其中一等奖的人数不少于30人,且不超过60人,这次奖励一等学生多少人时,购买奖品金额最少,最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.
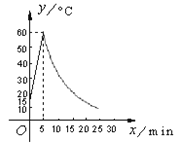
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
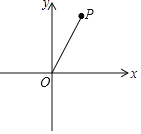
【题目】如图,在平面直角坐标系xOy中,点P坐标为(1,![]() ),以OP为斜边作等腰直角△OAP,直角顶点A在反比例函数y=
),以OP为斜边作等腰直角△OAP,直角顶点A在反比例函数y=![]() 的图象上,则k的值是_____.
的图象上,则k的值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com