
【题目】下列各式中,计算正确的是( )
A.3﹣1=﹣3
B.3﹣3=﹣9
C.3﹣2= ![]()
D.30=0
【答案】C
【解析】解:A、3﹣1= ![]() ≠﹣3,本选项不符合题意;
≠﹣3,本选项不符合题意;
B、3﹣3= ![]() ≠﹣9,本选项不符合题意;
≠﹣9,本选项不符合题意;
C、3﹣2= ![]() ,本选项符合题意;
,本选项符合题意;
D、30=1≠0,本选项不符合题意.
所以答案是:C.
【考点精析】认真审题,首先需要了解零指数幂法则(零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数)),还要掌握整数指数幂的运算性质(aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数))的相关知识才是答题的关键.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】(1)填写下表,观察被开方数a的小数点与算术平方根![]() 的小数点的移动规律:
的小数点的移动规律:
a | 0.0016 | 0.16 | 16 | 1600 |
|
(2)根据你发现的规律填空:
①已知:![]() =2.683 ,
=2.683 ,![]() 则
则![]() =_________,
=_________, ![]() =________
=________
②已知: ![]() =6.164,若
=6.164,若![]() =61.64, 则x=____________,
=61.64, 则x=____________,
(3)直接写出![]() 与a的大小.
与a的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市的空气质量情况,某环保兴趣小组从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计.根据空气污染指数的不同,将空气质量分为A、B、C、D和E五个等级,分别表示空气质量优、良、轻度污染、中度污染、重度污染,并绘制了如下两幅不完整的统计图.根据图中的信息,解答下列问题:
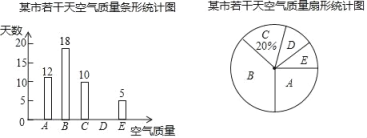
(1)求被抽取的天数;
(2)补全条形统计图,并求扇形统计图中表示空气质量为中度污染的扇形的圆心角度数;
(3)在这次抽取的天数中,求空气质量为良占的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
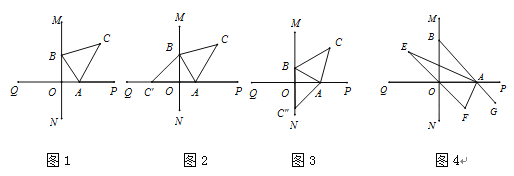
【题目】直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B在射线OM上运动,连接AB.
(1)如图,已知AC、BC分别是∠BAP和∠ABM角的平分线,
①点A、B在运动的过程中,∠ACB的大小是否发生变化?若发生变化,请说明理由;若不发生变化,试求出∠ACB的大小.
②如图,将△ABC沿直线AB折叠,若点C落在直线PQ上,记作点C′,则∠ABO= °;如图,将△ABC沿直线AB折叠,若点C落在直线MN上,记作点C′′,则∠ABO= °.
(2)如图,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线交于E、F,在△AEF中,如果有一个角是另一个角的![]() 倍,求∠ABO的度数.
倍,求∠ABO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
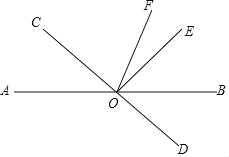
【题目】如图,直线AB,CD交于点O,OB平分∠DOE,OF是∠BOC的角平分线.
(1)说明:∠AOC=∠BOE;
(2)若∠AOC=46°,求∠EOF的度数;
(3)若∠EOF=30°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
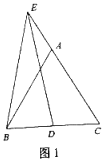
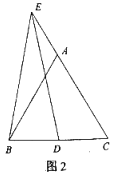
【题目】如图1,△ABC是等边三角形,点D是BC上一点,点E在CA的延长线上,连结EB、ED,且EB=ED.
(1)求证:∠DEC=∠ABE;
(2)点D关于直线EC的对称点为M,连接EM、BM:
①依题意将图2补全;
②求证:EB=BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
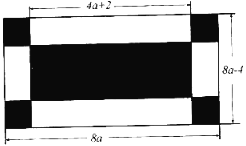
【题目】如图,某小区有一块长为![]() 米、宽为
米、宽为![]() 米的长方形地块该长方形地块。该长方形地块正中间是一个长为
米的长方形地块该长方形地块。该长方形地块正中间是一个长为![]() 米的长方形,四个角是大小相同的正方形,该小区计划
米的长方形,四个角是大小相同的正方形,该小区计划
将如图阴影部分进行绿化,对四个角的四个正方形采用A绿化方案,对正中间的长方形采用B绿化方案.
(1)采用A绿化方案的每个正方形边长是多少米,采用B绿化方案的长方形另一边长是多少米(用含![]() 的代数式表示);
的代数式表示);
(2)若采用A、B两种绿化方案的总造价相同,均为2700元,请你判断哪种方案单位面积造价高?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD边上的一动点,它从点A出发沿着A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com