
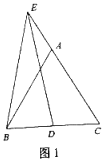
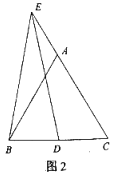
【题目】如图1,△ABC是等边三角形,点D是BC上一点,点E在CA的延长线上,连结EB、ED,且EB=ED.
(1)求证:∠DEC=∠ABE;
(2)点D关于直线EC的对称点为M,连接EM、BM:
①依题意将图2补全;
②求证:EB=BM.
【答案】(1)证明见解析;(2)①作图见解析;②证明见解析.
【解析】
(1)根据等边三角形的性质得到∠ABC=∠ACB=∠BAC=60°,再根据等边对等角以及三角形外角的性质即可得出结论;
(2)①根据题意作出图形即可;
②由轴对称的性质得到:DE=EM,DG=GM,再根据等腰三角形三线合一的性质得到∠2=∠1.由(1)的结论即可得到∠1=∠3.再证明△BEM是等边三角形即可得出结论.
(1)∵△ABC是等边三角形,∴∠ABC=∠ACB=∠BAC=60°.
∵BE=DE,∴∠EBD=∠EDB,∴∠EBA+∠ABC=∠CED+∠C,∴∠EBA =∠CED,即∠DEC=∠ABE;
(2)①作图如下:
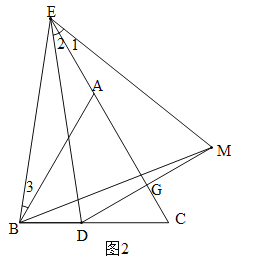
②∵D、M关于直线AC对称,∴DE=EM,DG=GM,∴∠2=∠1.由(1)得:∠2=∠3,∴∠1=∠3.
∵BE=DE,∴BE=ME.
∵∠3+∠BEA=∠BAC=60°,∴∠1+∠BEA=60°,∴∠BEM=60°.
∵BE=ME,∴△BEM是等边三角形,∴EB=BM.


科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AE=6,CE=2 ![]() ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图),然后将剩余部分拼成一个长方形(如图).

(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2-2ab+b2=(a-b)2 B.a2-b2=(a+b)(a-b) C.a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值.
②计算:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )(1-
)(1-![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制成如下统计图表(单位:cm):
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
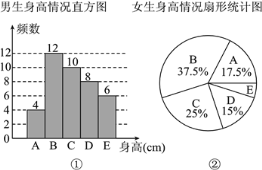
根据图表提供的信息,样本中,身高在160≤x<170之间的女生人数为( )
A. 8 B. 6 C. 14 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分5分)画图并填空:
如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.
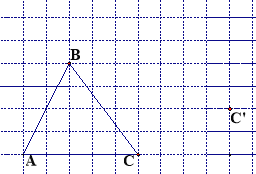
(1)画出平移后的△A′B′C′,(利用网格点和三角板画图)
(2)画出AB边上的高线CD;
(3)画出BC边上的中线AE;
(4)在平移过程中高CD扫过的面积为 .(网格中,每一小格单位长度为1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( ) ①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5米,A、B、C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3米,小明身高1.6米,则凉亭的高度AB约为( ) 
A.8.5米
B.9米
C.9.5米
D.10米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com