
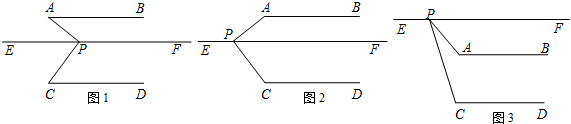
分析 (1)∠APC=∠A+∠C,利用两直线平行,内错角相等来证明;
(2)∠APC+∠A+∠C=360°,利用两直线平行,同旁内角互补来证明;
(3)∠PAB=∠PCD+∠APC,利用两直线平行,同旁内角互补来证明.
解答 解:(1)∠APC=∠A+∠C.
证明:∵线段AB∥CD,直线EF∥AB,
∴∠A=∠APE,∠C=∠CPE,
∵∠APC=∠APE+∠CPE,
∴∠APC=∠A+∠C.
(2)∠APC+∠A+∠C=360°.
证明:∵线段AB∥CD,直线EF∥AB,
∴∠A+∠APF=180°,∠C+∠CPF=180°,
∴∠A+∠APF+∠C+∠CPF=∠A+∠C+∠APC=360°
(3)∠PAB=∠PCD+∠APC.
证明:∵线段AB∥CD,直线EF∥AB,
∴∠APF+∠PAB=180°,∠CPF+∠PCD=180°,
∵∠APC=∠CPF-∠APF,
∴∠CPF+∠PCD-(∠APF+∠PAB)=(∠CPF-∠APF)+∠PCD-∠PAB=0°,
∴∠PAB=∠PCD+∠APC.
点评 本题考查了平行线的性质,解题的关键是:(1)两直线平行,内错角相等;(2)两直线平行,同旁内角互补;(3)两直线平行,同旁内角互补.本题属于基础题,难度不大,根据平行线的性质结合角之间的关系即可得以解决.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 4,6,1,7 | B. | 4,1,6,7 | C. | 6,4,1,7 | D. | 1,6,4,7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,Rt△ABC中,∠C=90°,AC=6,BC=8,AD平分∠BAC,则点B到AD的距离是( )
如图,Rt△ABC中,∠C=90°,AC=6,BC=8,AD平分∠BAC,则点B到AD的距离是( )| A. | 3 | B. | 4 | C. | 2$\sqrt{5}$ | D. | $\frac{{12\sqrt{13}}}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
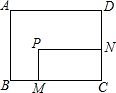 如图,矩形ABCD,AB=6,AD=8;动点M、N从点C出发,分别沿CB、CD以每秒2个单位长度和每秒1个单位长度的速度运动,分别至点B、点D停止.作矩形PMCN.若运动时间为x(单位:s),设矩形ABCD除去矩形PMCN后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是( )
如图,矩形ABCD,AB=6,AD=8;动点M、N从点C出发,分别沿CB、CD以每秒2个单位长度和每秒1个单位长度的速度运动,分别至点B、点D停止.作矩形PMCN.若运动时间为x(单位:s),设矩形ABCD除去矩形PMCN后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是( )| A. | 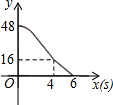 | B. | 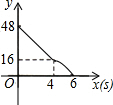 | C. | 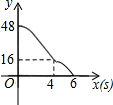 | D. | 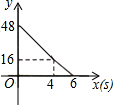 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
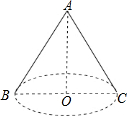 如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)△ABC是直角三角形,则圆锥的侧面展开图扇形的圆心角度约为( )
如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)△ABC是直角三角形,则圆锥的侧面展开图扇形的圆心角度约为( )| A. | 127° | B. | 180° | C. | 201° | D. | 255° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com