练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
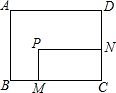
    4．如图，矩形ABCD，AB=6，AD=8；动点M、N从点C出发，分别沿CB、CD以每秒2个单位长度和每秒1个单位长度的速度运动，分别至点B、点D停止．作矩形PMCN．若运动时间为x（单位：s），设矩形ABCD除去矩形PMCN后剩余部分的面积为y（单位：cm2），则y与x之间的函数关系用图象表示大致是（　　）
    A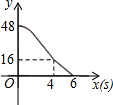．B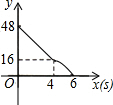．C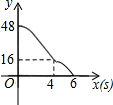．D．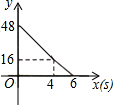

    分析 根据题意知，剩余部分面积分两种情况：①点M在CB上运动、点N在CD运动时，即0≤x≤4；②点M到达终点B、点N在CD上运动时，即4＜x≤6；根据以上两种情况分别用矩形ABCD的面积减去矩形PMCN的面积列出函数关系式可得答案．

    解答 解：根据题意，CM=2x，CN=x
    当0≤x≤4时，y=6×8-2x•x=-2x2+48，
    此时y与x满足二次函数关系；
    当4＜x≤6时，y=6×8-8×x=-8x+48，
    此时y与x满足一次函数关系；
    故选：A．

    点评 本题主要考查动点问题的函数图象，根据题意分类讨论是前提和基础，在两种前提下根据相等关系列出函数关系式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

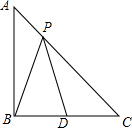    14．已知：如图，在等腰Rt△ABC中，∠ABC=90°，AB=2，D为BC的中点，P为线段AC上任意一点，则PB+PD的最小值为$\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．人造地球卫星要绕地球旋转，必须克服地球引力，克服地球引力的速度称为逃逸速度，逃逸速度的计算公式为$v=\sqrt{gR}$（千米/秒），其中g=0.0098千米/秒2，R=6370千米，求逃逸速度．（结果保留2个有效数字）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知线段AB∥CD，直线EF∥AB，若点P在直线EF上，连接PA、PC．
    （1）如图1，直线EF在线段AB、CD之间，点P在中间位置时，写出∠A、∠C、∠APC三个角之间的数量关系，并证明你的结论；
    （2）如图2，直线EF在线段AB、CD之间，点P在偏左位置时，写出∠A、∠C、∠APC三个角之间的数量关系，并证明你的结论；
    （3）如图3，直线EF在线段AB上方，点P在偏左位置时，写出∠PAB、∠PCD、∠APC三个角之间的数量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

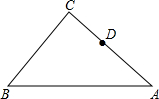    19．如图，在Rt△ABC中，∠C=90°，AC=14，tanA=$\frac{3}{4}$，点D是边AC上一点，AD=8，点E是边AB上一点，以点E为圆心，EA为半径作圆，经过点D，点F是边AC上一动点（点F不与A、C重合），作FG⊥EF，交射线BC于点G．
    （1）用直尺圆规作出圆心E，并求圆E的半径长（保留作图痕迹）；
    （2）当点G的边BC上时，设AF=x，CG=y，求y关于x的函数解析式，并写出它的定义域；
    （3）联结EG，当△EFG与△FCG相似时，推理判断以点G为圆心、CG为半径的圆G与圆E可能产生的各种位置关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如果一个三角形的三边长为5、12、13，与其相似的三角形的最长的边长为39，那么较大的三角形的面积为（　　）
    A．90B．180C．270D．540

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．某校九（1）班进行了一次体育测试，期中第一小组的成绩分别是（单位：分）30，25，29，28，28，30，29，28，20，28，27，30．这组数据的众数和中位数分别是（　　）
    A．28分，28分B．30分，28分C．28分，27.5分D．30分，27.5分

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

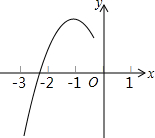    13．已知抛物线y=ax2+bx+c的顶点为D（-1，3），与x轴的一个交点在（-3，0）和（-2，0）之间，其部分图象如图，则以下结论：
    ①b2-4ac＞0；②c-a=3；③a+b+c＜0；④方程ax2+bx+c=m（m≥2）一定有实数根，其中正确的结论为（　　）
    A．②③B．①③C．①②③D．①②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．某水果店计划购进苹果和丑桔共140千克，这两种水果的进价、售价如表所示：
      进价（元/千克）售价（元/千克）
     苹果 5 8
     丑桔 9 13
    （1）若该水果店购进这两种水果的进货款为1000元，求水果店购进这两种水果各多少千克．
    （2）若该水果店决定丑桔的进货量不超过苹果进货量的3倍，应怎样安排进货才能使水果店在销售完这批水果时获利最多？

    查看答案和解析>>

    同步练习册答案