
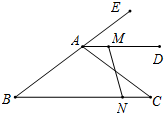
 如图,在△ABC中,AB=5cm,BC=8cm,AD为△ABC的外角平分线,且AD∥BC,点M从A出发,以1cm/s的速度沿射线AD匀速运动,同时点N以相同的速度从C出发沿CB匀速向点B运动,当点N到达B时,点M也停止运动.
如图,在△ABC中,AB=5cm,BC=8cm,AD为△ABC的外角平分线,且AD∥BC,点M从A出发,以1cm/s的速度沿射线AD匀速运动,同时点N以相同的速度从C出发沿CB匀速向点B运动,当点N到达B时,点M也停止运动.分析 (1)由条件可证明四边形AMCN为平行四边形,当MN垂直AC时,则四边形AMCN为菱形,在△ABN中,利用三角形三边关系可得到t的范围,可知存在满足条件的t,可得出结论;
(2)用t表示出CN,分CM=CN,MN=CN和CM=MN三种情况分别讨论,得出关于t的方程,求解即可.
解答 解:(1)如图,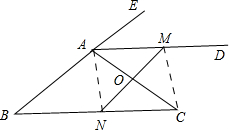
∵AD∥BC,
∴∠DAC=∠C,∠EAD=∠B,
∵AD平分∠EAC,
∴∠EAD=∠CAD,
∴∠B=∠C,
∴AB=AC=5,
∵BC=8
∴cos∠C=$\frac{4}{5}$
如图,连接AN,CM,
∵M、N的速度相等,
∴AM=CN=t,且AM∥CN,
∴四边形AMCN为平行四边形,
当MN⊥AC时,$\frac{OC}{CN}$=$\frac{4}{5}$,OC=$\frac{5}{2}$,t=$\frac{25}{8}$
∴存在使四边形AMCN为菱形的时间t,即MN可以垂直平分AC;
(2)①由(1)可知,当四边形AMCN为菱形时,即CM=CN,此时t=$\frac{25}{8}$;
②当MN=NC时,如图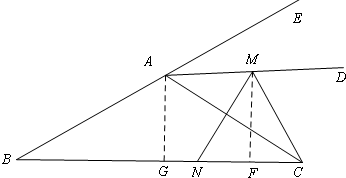
过A点作AG⊥BC于点G,过点M作MF⊥BC于点F,
由(1)知△ABC为等腰三角形,
∴BG=CG=4cm,
∵AD∥BC
∴四边形AGFM为矩形,
在Rt△ABG中由勾股定理得AG=3
∴AM=GF=t,AG=MF=3
若MN=NC=t
则NF=GF-(CG-NG)=t-(4-t)=2t-4;
在Rt△MNF中由勾股定理得:NF2+MF2=MN2
即(2t-4)2+32=t2
整理得:3t2-16t+25=0,此方程无解
故不存在MN=NC;
③当MN=MC时,如图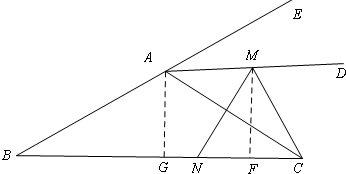
过A点作AG⊥BC于点G,过点M作MF⊥BC于点F,
由(1)知△ABC为等腰三角形,
∴BG=CG=4cm,
∵AD∥BC
∴四边形AGFM为矩形,
在Rt△ABG中由勾股定理得AG=3
∴AM=GF=t,AG=MF=3
若MN=MC=t
则CF=$\frac{1}{2}$CN=$\frac{1}{2}$t
又CF=CG-FG=4-t
∴$\frac{1}{2}$t=4-t
解得:t=$\frac{8}{3}$
∴当t为$\frac{25}{8}$或$\frac{8}{3}$时△MNC为等腰三角形.
点评 本题考查了等腰三角形的性质,线段垂直平分线性质,三角形内角和定理的应用,能得出关于x的方程是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等,等边对等角.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:填空题
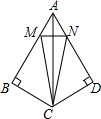 如图,在△ABC中,AB⊥BC,将△ABC沿着AC折叠,得到△ADC,点M、N分别在AB、AD边上,且AM=AN=$\frac{1}{3}$AB,连接MN,若∠BAD=60°,则tan∠MNC的值为3$\sqrt{3}$.
如图,在△ABC中,AB⊥BC,将△ABC沿着AC折叠,得到△ADC,点M、N分别在AB、AD边上,且AM=AN=$\frac{1}{3}$AB,连接MN,若∠BAD=60°,则tan∠MNC的值为3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
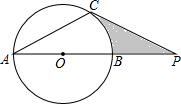 已知:如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
已知:如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,线段AB上有一任意点C,点M是线段AC的中点,点N是线段BC的中点,当AB=6cm时,
如图,线段AB上有一任意点C,点M是线段AC的中点,点N是线段BC的中点,当AB=6cm时,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
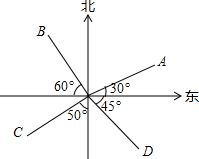 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | OA的方向是北偏东30° | B. | OB的方向是北偏西60° | ||
| C. | OC的方向是南偏东50° | D. | OD的方向是东偏南45° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
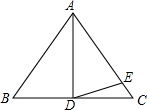 如图,在△ABC中,AB=AC,AD是边BC上的高,E为AC边上一点,且有AE=AD,∠EDC=22°,则∠B的度数为( )
如图,在△ABC中,AB=AC,AD是边BC上的高,E为AC边上一点,且有AE=AD,∠EDC=22°,则∠B的度数为( )| A. | 44° | B. | 46° | C. | 56° | D. | 54° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com