
分析 设个位数字为x,十位上的数字为y,则百位上的数字为x+y,根据“交换百位与十位上的数字位置后,得到的三位数比原来小90,”“交换十位与个位数字的位置后,得到的三位数比原三位数小9,”列出方程组解答问题即可.
解答 解:设个位数字为x,十位上的数字为y,由题意得
$\left\{\begin{array}{l}{100(x+y)+10y=100y+10(x+y)+90}\\{10y+x=10x+y+9}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$
则x+y=3
原来的三位数是321.
答:原来的三位数是321.
点评 本题考查了二元一次方程组的应用,掌握数的表示要用数位上的数字乘以数位的计数单位是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 经过点(2,2) | B. | y随x的增大而增大 | ||
| C. | 两个分支分布在二、四象限 | D. | 图象关于x轴对称 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
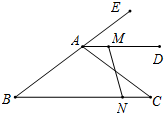 如图,在△ABC中,AB=5cm,BC=8cm,AD为△ABC的外角平分线,且AD∥BC,点M从A出发,以1cm/s的速度沿射线AD匀速运动,同时点N以相同的速度从C出发沿CB匀速向点B运动,当点N到达B时,点M也停止运动.
如图,在△ABC中,AB=5cm,BC=8cm,AD为△ABC的外角平分线,且AD∥BC,点M从A出发,以1cm/s的速度沿射线AD匀速运动,同时点N以相同的速度从C出发沿CB匀速向点B运动,当点N到达B时,点M也停止运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com