
【题目】已知一次函数y=kx+b的图象与x轴交于点A(-2,0),与y轴交于点B.若△AOB的面积为8,求一次函数的表达式.
【答案】一次函数的表达式是y=4x+8或y=-4x-8.
【解析】
根据图象经过点A(-2,0),可得0=-2k+b,进而得到b=2k,再根据△AOB的面积为8可得:![]() ×2×|b|=8,进而算出|b|的值,再计算出b,然后把b的值代入b=2k即可算出答案.
×2×|b|=8,进而算出|b|的值,再计算出b,然后把b的值代入b=2k即可算出答案.
∵一次函数y=kx+b的图象经过点A(-2,0),
∴0=-2k+b,∴b=2k.①
∵一次函数y=kx+b的图象与y轴的交点是B(0,b),
∴S△AOB=![]() OA·OB=8,
OA·OB=8,
即![]() ×2×|b|=8,
×2×|b|=8,
∴|b|=8,∴b1=8,b2=-8.
将b1=8,b2=-8分别代入①式,得k1=4,k2=-4,
∴一次函数的表达式是y=4x+8或y=-4x-8.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】A、B两地相距400km,甲、乙两车分别从A、B两地同时出发,相向而行,甲车以每小时100km的速度匀速行驶1h后,休息了1h,然后按原速继续行驶到B地,乙车以每小时80km的速度匀速行驶到A地.
(1)当乙车经过甲车休息的地方时,乙车行驶的时间是 h;
(2)当甲、乙两车相遇时,求乙车行驶的时间;
(3)当甲、乙两车相距40km时,求乙车行驶的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆O通过五边形OABCD的四个顶点.若 ![]() =150°,∠A=65°,∠D=60°,则
=150°,∠A=65°,∠D=60°,则 ![]() 的度数为何?( )
的度数为何?( ) 
A.25
B.40
C.50
D.55
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,M、E、F三点在 ![]() 上,N是矩形两对角线的交点.若
上,N是矩形两对角线的交点.若 ![]() =24,
=24, ![]() =32,
=32, ![]() =16,
=16, ![]() =8,
=8, ![]() =7,则下列哪一条直线是A、C两点的对称轴?( )
=7,则下列哪一条直线是A、C两点的对称轴?( ) 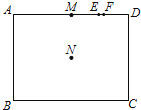
A.直线MN
B.直线EN
C.直线FN
D.直线DN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形 ABCD 中,AB=6cm,BC=3cm,E 为 CD 的中点.动点 P 从 A 点出发,以每秒1cm 的速度沿 A﹣B﹣C﹣E 运动,最终到达点 E.若点 P 运动时间为 x 秒,则 x=_______时,△APE 的面积等于 6.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
日期x | 1 | 2 | 3 | 4 |
水位y(米) | 20.0 | 20.5 | 21.0 | 21.5 |
(1)请建立该水库水位y(米)与日期x之间的函数模型,求出函数表达式;
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?请简要说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
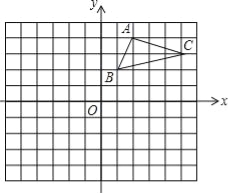
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.
【答案】(1)作图见解析;点A1的坐标(2,﹣4);(2)作图见解析;点A2的坐标(﹣2,4).
【解析】
试题分析:(1)分别找出A、B、C三点关于x轴的对称点,再顺次连接,然后根据图形写出A点坐标;
(2)将△A1B1C1中的各点A1、B1、C1绕原点O旋转180°后,得到相应的对应点A2、B2、C2,连接各对应点即得△A2B2C2.
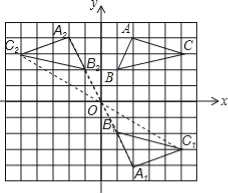
试题解析:(1)如图所示:点A1的坐标(2,﹣4);
(2)如图所示,点A2的坐标(﹣2,4).
考点:1.作图-旋转变换;2.作图-轴对称变换.
【题型】解答题
【结束】
18
【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.
![]()
①1=1 ②1+2=![]() =3 ③1+2+3=
=3 ③1+2+3=![]() =6 ④ …
=6 ④ …
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.
![]()
1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通过猜想,写出(2)中与第n个点阵相对应的等式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
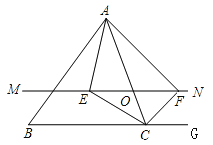
【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com