
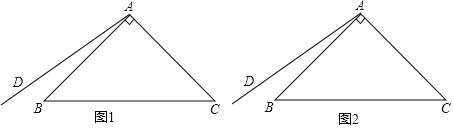
【题目】已知△ABC中,∠BAC=90°,AB=AC,在△ABC外侧作射线AD,点B关于射线AD的对称点为E,连接CE,CE交射线AD与点F.
(1)依题意补全如图.
(2)设∠BAD=α,若0°<α<45°,求∠AEC的大小(用含α的代数式表示).
(3)如图,0°<∠BAD<45°,用等式表示线段EC,FC与EB之间的数量关系.
【答案】(1)补图见解析;(2)∠AEC==45°-α.证明见解析;(3)EB=![]() (EC-FC),证明见解析.
(EC-FC),证明见解析.
【解析】
(1)根据要求画出图形即可.
(2)首先证明∠EAC=90°+2α,理由等腰三角形的性质即可解决问题.
(3)结论:EB=![]() (EC-FC).想办法证明△EFB是等腰直角三角形即可解决问题.
(EC-FC).想办法证明△EFB是等腰直角三角形即可解决问题.
(1)所画图形,如图所示.
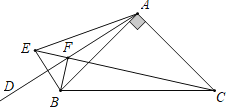
(2)∵点B关于射线AD的对称点为E,
∴∠EAD=∠BAD=α,
∵∠BAC=90°,
∴∠EAC=90°+2α,
∵AE=AB=AC,
∴∠AEC=![]() (180°-90°-2α)=45°-α.
(180°-90°-2α)=45°-α.
(3)结论:结论:EB=![]() (EC-FC).
(EC-FC).
理由:∵∠EFD=∠AEC+∠AEF=45°-α+α=45°,
∵AD垂直平分线段BE,
∴∠BFD=∠EFD=45°,
∴∠EFB=90°,∵FE=FB,
∴△EFB是等腰直角三角形,
∴EC-CF=EF=![]() EB,
EB,
∴EB=![]() (EC-FC).
(EC-FC).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】2019年8月.山西龙城将迎来全国第二届青年运动会,盛会将至,整个城市已经进入了全力准备的状态.太职学院足球场作为一个重要比赛场馆.占地面积约24300平方米.总建筑面积4790平方米,设有2476个座位,整体建筑简洁大方,独具特色.2018年3月15日该场馆如期开工,某施工队负责安装该场馆所有座位,在安装完476个座位后,采用新技术,效率比原来提升了![]() .结来比原计划提前4天完成安装任务.求原计划每天安装多少个座位.
.结来比原计划提前4天完成安装任务.求原计划每天安装多少个座位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商城销售A,B两种自行车.A型自行车售价为2 100元/辆,B型自行车售价为1 750元/辆,每辆A型自行车的进价比每辆B型自行车的进价多400元,商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等.
(1)求每辆A,B两种自行车的进价分别是多少?
(2)现在商城准备一次购进这两种自行车共100辆,设购进A型自行车m辆,这100辆自行车的销售总利润为y元,要求购进B型自行车数量不超过A型自行车数量的2倍,总利润不低于13 000元,求获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
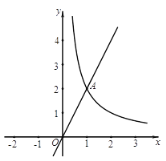
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与函数
与函数![]() 的图象交于点A(1,2).
的图象交于点A(1,2).
(1)求![]() 的值;
的值;
(2)过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,直线
,直线![]() 与直线l交于点B,与函数
与直线l交于点B,与函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点D.
轴交于点D.
①当点C是线段BD的中点时,求![]() 的值;
的值;
②当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD交于点O,以OC,OD为邻边作平行四边形OCED,连接OE.
(1)求证:四边形OBCE是平行四边形;
(2)连接BE交AC于点F.若AB=2,∠AOB=60°,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
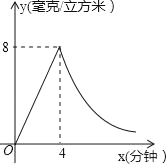
【题目】为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克/立方米)与药物点燃后的时间x(分钟)成正比例,药物燃尽后,y与x成反比例(如图所示).已知药物点燃后4分钟燃尽,此时室内每立方米空气中含药量为8毫克.
(1)求药物燃烧时,y与x之间函数的表达式;
(2)求药物燃尽后,y与x之间函数的表达式;
(3)研究表明,当空气中每立方米的含药量不低于2毫克时,才能有效杀灭空气中的病菌,那么此次消毒有效时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:

(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?
(3)小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
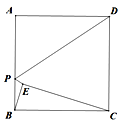
【题目】如图,正方形ABCD的边长为6,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是边AB上一动点,连接PD,PE,则PD+PE的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com