
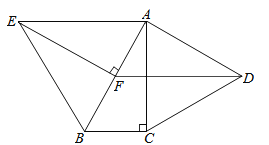
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF.
(1)求证:△ABC≌△EAF;
(2)试判断四边形EFDA的形状,并证明你的结论.
【答案】(1)证明见解析;(2)四边形EFDA是平行四边形.
【解析】
试题分析:(1)由△ABE是等边三角形可知:AE=BE,∠EAF=60°,于是可得到∠EFA=∠ACB,∠EAF=∠ABC,接下来依据AAS证明△ABC≌△EAF即可;
(2)由△ABC≌△EAF可得到EF=AC,由△ACD是的等边三角形进而可证明AC=AD,然互再证明∠BAD=90°,可证明EF∥AD,故此可得到四边形EFDA为平行四边形.
试题解析:(1)证明:∵△ABE是等边三角形,EF⊥AB,∴∠EAF=60°,AE=BE,∠EFA=90°.
又∵∠ACB=90°,∠ABC=60°,∴∠EFA=∠ACB,∠EAF=∠ABC.
在△ABC和△EAF中,∵∠EFA=∠ACB,∠EAF=∠ABC,AE=BE,∴△ABC≌△EAF.
(2)结论:四边形EFDA是平行四边形.
理由:∵△ABC≌△EAF,∴EF=AC.∵△ACD是的等边三角形,∴AC=AD,∠CAD=60°,∴AD=EF.又∵Rt△ABC中,∠ABC=60°,∠BAC=30°,∴∠BAD=∠BAC+∠CAD=90°,∴∠EFA=∠BAD=90°,∴EF∥AD.又∵EF=AD,∴四边形EFDA是平行四边形.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(3,2)、(﹣1,0),若将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标为 . 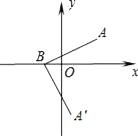
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要想了解10万名考生的数学成绩,从中抽取了2000名考生的数学成绩进行统计分析,以下说法正确的是 ( )
A、这2000名考生是总体的一个样本 B、每位考生的数学成绩是个体
C、10万名考生是个体 D、2000名考生是样本的容量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算中,错误的是( )
A. 3a﹣2a=a B. ﹣2a(3a﹣1)=﹣6a2﹣1 C. ﹣8a2÷2a=﹣4a D. (a+3b)2=a2+6ab+9b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上四个点A,B,C,D. 按要求完成下列问题: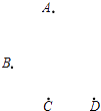
(1)①连接AC,BD;②画射线AB与直线CD相交于点E;
(2)用量角器度量∠AED的大小为(精确到度).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com