
 如图,在Rt△ABC中,∠B=90°,∠A的平分线与BC相交于点D,点E在AB上,DE=DC,以D为圆心,DB长为半径作⊙D.
如图,在Rt△ABC中,∠B=90°,∠A的平分线与BC相交于点D,点E在AB上,DE=DC,以D为圆心,DB长为半径作⊙D.分析 (1)过D作DF⊥AC于F,如图,利用角平分线的性质定理可得到DF=DB,则根据切线的判定方法可判断AC是⊙D的切线;
(2)先判断AB是圆D的切线,则根据切线长定理得到AB=AF,再证明△BDE≌△FDC得到BE=CF,于是得到AC=AF+CF=AB+BE.
解答 解:(1)AC与⊙D相切.理由如下:
过D作DF⊥AC于F,如图,
∵AD平分∠BAC,∠B=∠AFD=90°,
∴DF=DB,
∴AC是⊙D的切线;
(2)∵∠B=90°,DB为半径,
∴AB是圆D的切线,
∴AB=AF,
在Rt△BDE与Rt△FDC中,
$\left\{\begin{array}{l}{DE=CD}\\{DB=DF}\end{array}\right.$
∴△BDE≌△FDC(HL),
∴BE=CF,
∴AC=AF+CF=AB+BE.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.灵活应用角平分线的性质定理和运用全等三角形的知识解决线段相等的问题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 图形个数( n ) | (1) | (2) | (3) |
| 正方形的个数 | 8 | 13 | 18 |
| 图形的周长 | 18 | 28 | 38 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
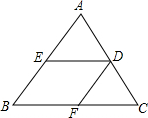 如图,在△ABC中,DE∥BC,DF∥AB,那么下列比例式中正确的是①;(填序号)
如图,在△ABC中,DE∥BC,DF∥AB,那么下列比例式中正确的是①;(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:一长为32m、宽为20m的矩形地面上修建有同样宽的道路(图中阴影部分)余下部分进行了绿化,若已知绿化面积为540m2,求道路的宽.
如图:一长为32m、宽为20m的矩形地面上修建有同样宽的道路(图中阴影部分)余下部分进行了绿化,若已知绿化面积为540m2,求道路的宽.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是由7个相同的小立方体组成的几何体,
如图是由7个相同的小立方体组成的几何体,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com