
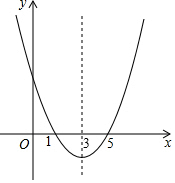 二次函数y=ax2+bx+c的图象如图,对称轴为直线x=3,且当x1=$\sqrt{2}$时函数值为y1;x2=π时函数值为y2;当x3=0时函数值为y3;则y1、y2、y3的大小关系是y2<y1<y3.
二次函数y=ax2+bx+c的图象如图,对称轴为直线x=3,且当x1=$\sqrt{2}$时函数值为y1;x2=π时函数值为y2;当x3=0时函数值为y3;则y1、y2、y3的大小关系是y2<y1<y3. 科目:初中数学 来源: 题型:解答题
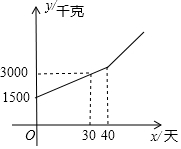 某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在刚种植和第30天的需水量分别为1500千克和3000千克,在第40天后每天的需水量比前一天增加100千克.
某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在刚种植和第30天的需水量分别为1500千克和3000千克,在第40天后每天的需水量比前一天增加100千克.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com