
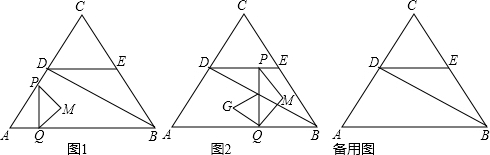
分析 (1)如图1中,作DT⊥AB于T,EN⊥AB于N,CH⊥AB于H,MK⊥PQ于K,则四边形DENT是矩形,当点M在BD上时,由PK=KQ,KM∥AB,推出DM=MB,易知KM=PK=KQ=2,DP=2,由此即可解决问题.
(2)分四种情形讨论①如图2中,作DT⊥AB于T,当0<t≤5时,重叠部分是△PQM.②如图3中,当5<t≤7时,重叠部分是四边形QMHK.取BD的中点M′,作M′P′∥PM交DE于P′.③如图4中,当7<t≤10时,重叠部分是△QHK.GK,M′G′分别是△QHK、△Q′H′M′的高.④如图5中,10<t≤$\frac{85}{6}$时,重叠部分是△QKH.分别求解即可.
(3)存在.分三种情形①如图6中,当FG=FQ时.②如图7中,当GF=GQ时,作GK⊥PQ,DN⊥AB于N.③如图8中,当QF=QG时,作QK⊥GF于K.DN⊥AB于N.分别求出PD的长即可解决问题.
解答 解:(1)如图1中,作DT⊥AB于T,EN⊥AB于N,CH⊥AB于H,MK⊥PQ于K,则四边形DENT是矩形,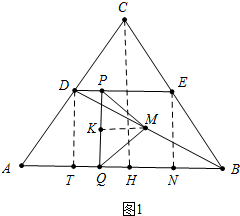
由△DTA≌△ENB,可得DE=NT=PQ=5,AT=BN=3,
∵AD=EB=5,
∴DT=EN=4,
当点M在BD上时,∵PK=KQ,KM∥AB,
∴DM=MB,易知KM=PK=KQ=2,DP=2,
∴t=7秒时,点M在BD上,
∵EN∥CH,
∴△ENB∽△CHB,
∴$\frac{EB}{CB}$=$\frac{BN}{BH}$,
∴$\frac{5}{BC}$=$\frac{3}{5.5}$,
∴BC=$\frac{55}{6}$,EC=$\frac{25}{6}$,
∴点P到达点C时间为:5+5+$\frac{25}{6}$=$\frac{85}{6}$秒.
故答案为7秒,$\frac{85}{6}$秒.
(2)①如图2中,作DT⊥AB于T,当0<t≤5时,重叠部分是△PQM,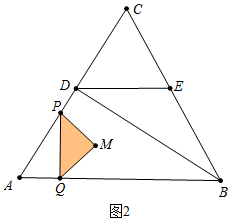
∵sinA=$\frac{PQ}{PA}$=$\frac{4}{5}$,
∴PQ=$\frac{4}{5}$t,
∴S=S△PQM=$\frac{1}{2}$•$\frac{4}{5}$t•$\frac{2}{5}$t=$\frac{4}{25}$t2.
②如图3中,当5<t≤7时,重叠部分是四边形QMHK.取BD的中点M′,作M′P′∥PM交DE于P′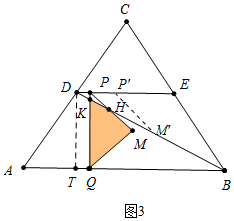
∵KQ∥DT,
∴$\frac{KQ}{DT}$=$\frac{BQ}{BT}$,
∴$\frac{KQ}{4}$=$\frac{13-t}{8}$,
∴KQ=$\frac{13-t}{2}$,PK=4-$\frac{13-t}{2}$=$\frac{t-5}{2}$,
∵P′M′∥PH,
∴$\frac{DH}{DM′}$=$\frac{DP}{DP′}$,
∴$\frac{DH}{2\sqrt{5}}$=$\frac{t-5}{2}$,
∴DH=$\sqrt{5}$(t-5),∵DK=$\frac{\sqrt{5}(t-5)}{2}$,
∴HK=DH-DK=$\frac{1}{2}$$\sqrt{5}$(t-5),
∴S=S△PMQ-S△PKH=4-$\frac{1}{2}$×$\frac{t-5}{2}$×$\frac{t-5}{2}$=-$\frac{1}{8}$t2+$\frac{5}{4}$t+$\frac{7}{8}$.
③如图4中,当7<t≤10时,重叠部分是△QHK.GK,M′G′分别是△QHK、△Q′H′M′的高.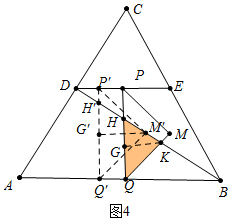
由△QHK∽△Q′H′M′,得到,$\frac{QH}{Q′H′}$=$\frac{GK}{G′M′}$,
∴$\frac{\frac{13-t}{2}}{3}$=$\frac{GK}{2}$,
∴GK=$\frac{13-t}{3}$,
∴S=$\frac{1}{2}$×$\frac{13-t}{2}$×$\frac{13-t}{3}$=$\frac{1}{12}$t2-$\frac{13}{6}$t+$\frac{169}{12}$.
④如图5中,10<t≤$\frac{85}{6}$时,重叠部分是△QKH.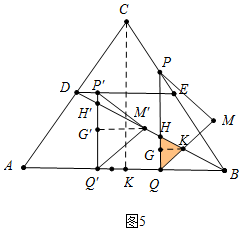
由△QHK∽△Q′H′M′,得$\frac{QH}{Q′H′}$=$\frac{GK}{M′G′}$,可得GK=$\frac{2}{3}${5-$\frac{1}{2}[5-\frac{3}{5}(t-10)]\}$,
∴S=$\frac{1}{2}$•HQ•GK=$\frac{1}{2}$•$\frac{2}{3}${5-$\frac{1}{2}[5-\frac{3}{5}(t-10)]\}$2=$\frac{3}{100}{t}^{2}$-$\frac{1}{10}$t+$\frac{1}{12}$.
综上所述,S=$\left\{\begin{array}{l}{\frac{4}{25}{t}^{2}}&{(0<t≤5)}\\{-\frac{1}{8}{t}^{2}+\frac{5}{4}t+\frac{7}{8}}&{(5<t≤7)}\\{\frac{1}{12}{t}^{2}-\frac{13}{6}t+\frac{169}{12}}&{(7<t≤10)}\\{\frac{3}{100}{t}^{2}-\frac{1}{10}t+\frac{1}{12}}&{(10<t≤\frac{85}{6})}\end{array}\right.$.
(3)存在.①如图6中,当FG=FQ时,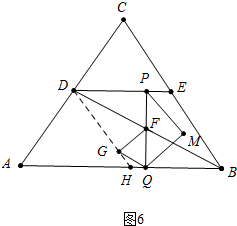
∵PF=FG=FQ=2,
∴DP=4,
∴t=5+4=9.
②如图7中,当GF=GQ时,作GK⊥PQ,DN⊥AB于N.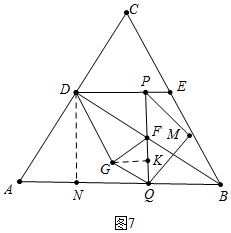
由△DAN∽△GFK,得$\frac{AD}{FG}$=$\frac{AN}{FK}$,
∴$\frac{5}{\frac{1}{2}(t-5)}$=$\frac{3}{FK}$,
∴FK=$\frac{3}{10}$(t-5),
∵GF=GQ,GK⊥FQ,
∴FQ=2FK=$\frac{3}{5}(t-5)$,
∵PF+FQ=4,
∴$\frac{1}{2}$(t-5)+$\frac{3}{5}$(t-5)=4,
∴t=$\frac{95}{11}$.
③如图8中,当QF=QG时,作QK⊥GF于K.DN⊥AB于N.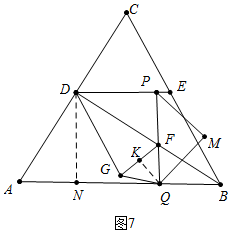
由△ADN∽△FQK,得到$\frac{AN}{FK}$=$\frac{AD}{FQ}$,
∴$\frac{3}{\frac{1}{4}(t-5)}$=$\frac{5}{FQ}$,
∴FQ=$\frac{5}{12}$(t-5),
∵PF+FQ=4,
∴$\frac{1}{2}$(t-5)+$\frac{5}{12}$(t-5)=4,
∴t=$\frac{103}{11}$,
综上所述,当△FGQ是等腰三角形时,t的值为9s或$\frac{95}{11}$s或$\frac{103}{11}$s.
点评 本题考查相似型综合题、相似三角形的判定和性质、三角形面积、等腰三角形的判定和性质等知识,解题的关键是学会分类讨论的思想思考问题,灵活应用相似三角形的性质,学会利用参数构建方程,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
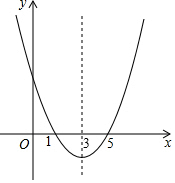 二次函数y=ax2+bx+c的图象如图,对称轴为直线x=3,且当x1=$\sqrt{2}$时函数值为y1;x2=π时函数值为y2;当x3=0时函数值为y3;则y1、y2、y3的大小关系是y2<y1<y3.
二次函数y=ax2+bx+c的图象如图,对称轴为直线x=3,且当x1=$\sqrt{2}$时函数值为y1;x2=π时函数值为y2;当x3=0时函数值为y3;则y1、y2、y3的大小关系是y2<y1<y3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
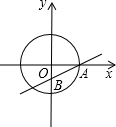 如图,在平面直角坐标系中,⊙O的直径2$\sqrt{3}$,直线AB的函数解析式为y=$\frac{\sqrt{3}}{3}$x-1,交坐标轴于点A和点B,将线段AB作平移变换,使所得的线段的两端都落在⊙O上,则平移后A点所对应的点的坐标($\frac{\sqrt{2}+\sqrt{3}}{2}$,$\frac{1-\sqrt{6}}{2}$)或($\frac{\sqrt{3}-\sqrt{2}}{2}$,$\frac{1+\sqrt{6}}{2}$).
如图,在平面直角坐标系中,⊙O的直径2$\sqrt{3}$,直线AB的函数解析式为y=$\frac{\sqrt{3}}{3}$x-1,交坐标轴于点A和点B,将线段AB作平移变换,使所得的线段的两端都落在⊙O上,则平移后A点所对应的点的坐标($\frac{\sqrt{2}+\sqrt{3}}{2}$,$\frac{1-\sqrt{6}}{2}$)或($\frac{\sqrt{3}-\sqrt{2}}{2}$,$\frac{1+\sqrt{6}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com