
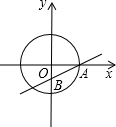
 如图,在平面直角坐标系中,⊙O的直径2$\sqrt{3}$,直线AB的函数解析式为y=$\frac{\sqrt{3}}{3}$x-1,交坐标轴于点A和点B,将线段AB作平移变换,使所得的线段的两端都落在⊙O上,则平移后A点所对应的点的坐标($\frac{\sqrt{2}+\sqrt{3}}{2}$,$\frac{1-\sqrt{6}}{2}$)或($\frac{\sqrt{3}-\sqrt{2}}{2}$,$\frac{1+\sqrt{6}}{2}$).
如图,在平面直角坐标系中,⊙O的直径2$\sqrt{3}$,直线AB的函数解析式为y=$\frac{\sqrt{3}}{3}$x-1,交坐标轴于点A和点B,将线段AB作平移变换,使所得的线段的两端都落在⊙O上,则平移后A点所对应的点的坐标($\frac{\sqrt{2}+\sqrt{3}}{2}$,$\frac{1-\sqrt{6}}{2}$)或($\frac{\sqrt{3}-\sqrt{2}}{2}$,$\frac{1+\sqrt{6}}{2}$). 分析 根据条件先计算图1中的直角△AOB的三边长,得∠BOA=30°;根据两直线平行的性质,同位角相等,可以得不管直线AB向上或向下平移与x轴夹角都是30°,分两种情况进行讨论:①当直线AB向下平移时,如图2,作辅助线,构建直角三角形及平移后的点A′与两坐标轴的垂线,由30°角的性质和三角函数求
出A′Q和OQ的长,写出点A′的坐标即可;②同理在图3中求出A′的坐标.
解答 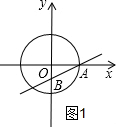 解:如图1,当x=0时,y=-1,
解:如图1,当x=0时,y=-1,
则B(0,-1),
当y=0时,$\frac{\sqrt{3}}{3}$x-1=0,x=$\sqrt{3}$,
则A($\sqrt{3}$,0),
Rt△AOB中,由勾股定理得:AB=2,
∴∠BAO=30°
分两种情况:
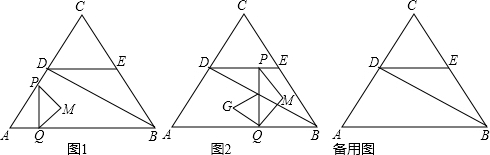
①当直线AB向下平移时,如图2,
由平移得:∠B′NO=30,
过O作OM⊥A′B′于M,连接OB′、OA′,过A作AQ⊥x轴于Q,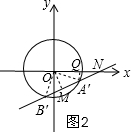
∵OB′=OA′=OA=$\sqrt{3}$,A′B′=AB=2,
∴A′M=B′M=1,
∴OM=$\sqrt{(\sqrt{3})^{2}-{1}^{2}}$=$\sqrt{2}$,
Rt△OMN中,ON=2OM=2$\sqrt{2}$,
∴MN=$\sqrt{(2\sqrt{2})^{2}-(\sqrt{2})^{2}}$=$\sqrt{6}$,
∴A′N=ON-OA′=$\sqrt{6}$-1,
∴AQ=$\frac{1}{2}$A′N=$\frac{\sqrt{6}-1}{2}$,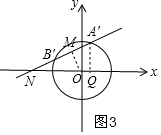
cos30°=$\frac{QN}{A′N}$,
∴QN=$\frac{\sqrt{3}}{2}$×($\sqrt{6}$-1)=$\frac{3\sqrt{2}-\sqrt{3}}{2}$,
∴OQ=ON-QN=2$\sqrt{2}$-$\frac{3\sqrt{2}-\sqrt{3}}{2}$=$\frac{\sqrt{2}+\sqrt{3}}{2}$,
∴A′($\frac{\sqrt{2}+\sqrt{3}}{2}$,$\frac{1-\sqrt{6}}{2}$);
②当直线AB向上平移时,如图3,
同理得A′($\frac{\sqrt{3}-\sqrt{2}}{2}$,$\frac{1+\sqrt{6}}{2}$)
则平移后A点所对应的点的坐标为:($\frac{\sqrt{2}+\sqrt{3}}{2}$,$\frac{1-\sqrt{6}}{2}$)或($\frac{\sqrt{3}-\sqrt{2}}{2}$,$\frac{1+\sqrt{6}}{2}$).
点评 本题考查了坐标与图形变换--平移,明确平移前后的两线段相等且平行,本题根据已知直线的解析式求出线段的长,得出30°角是关键,采用了分类讨论的思想,分别向上平移和向下平移;构建对应的直角三角形,与特殊的三角函数、勾股定理相结合得出结论.


科目:初中数学 来源: 题型:解答题
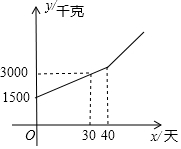 某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在刚种植和第30天的需水量分别为1500千克和3000千克,在第40天后每天的需水量比前一天增加100千克.
某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在刚种植和第30天的需水量分别为1500千克和3000千克,在第40天后每天的需水量比前一天增加100千克.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 1或2 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com