
【题目】三角板是学习数学的重要工具,将一副三角板中的两块直角三角板的直角顶点![]() 按如图方式叠放在一起,当
按如图方式叠放在一起,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,解决下列问题:(友情提示:
的上方时,解决下列问题:(友情提示:![]() ,
,![]() ,
,![]() .
.

(1)①若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
②若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)这两块三角板是否存在一组边互相平行?若存在,请直接写出![]() 的角度所有可能的值(不必说明理由);若不存在,请说明理由.
的角度所有可能的值(不必说明理由);若不存在,请说明理由.
【答案】(1)①135°②40°(2)∠ACB与∠DCE互补(3)存在一组边互相平行
【解析】
(1)①根据∠DCE和∠ACD的度数,求得∠ACE的度数,再根据∠BCE求得∠ACB的度数;②根据∠BCE和∠ACB的度数,求得∠ACE的度数,再根据∠ACD求得∠DCE的度数;
(2)根据∠ACE=90°-∠DCE以及∠ACB=∠ACE+90°,进行计算即可得出结论;
(3)分五种情况进行讨论:当CB∥AD时,当EB∥AC时,当CE∥AD时,当EB∥CD时,当BE∥AD时,分别求得∠ACE角度.
(1)①∵∠ACD=90°,∠DCE=45°,
∴∠ACE=45°,
∴∠ACB=90°+45°=135°,
故答案为:135°;
②∠ACB=140°,∠ACD=∠ECB=90°,
∴∠ACE=140°﹣90°=50°,
∴∠DCE=∠DCA﹣∠ACE=90°﹣50°=40°;
故答案为:40°;
(2)∠ACB与∠DCE互补.理由:
∵∠ACD=90°,
∴∠ACE=90°﹣∠DCE,
又∵∠BCE=90°,
∴∠ACB=90°+90°﹣∠DCE,
∴∠ACB+∠DCE=90°+90°﹣∠DCE+∠DCE=180°,
即∠ACB与∠DCE互补;
(3)存在一组边互相平行,
当∠ACE=45°时,∠ACE=∠E=45°,此时AC∥BE;
当∠ACE=30°时,∠ACB=120°,此时∠A+∠ACB=180°,故AD∥BC.


科目:初中数学 来源: 题型:
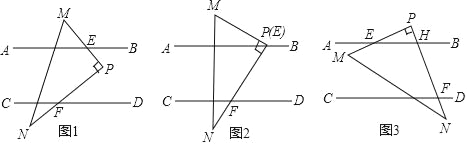
【题目】问题情境:已知:如图1,直线AB∥CD,现将直角三角板△PMN放入图中,其中∠MPN=90°,点P始终在直线MN右侧.PM交AB于点E,PN交CD于点F,试探究:∠PFD与∠AEM的数量关系.
(1)特例如图2,当点P在直线AB上(即点E与点P重合)时,直接写出∠PFD与∠AEM的数量关系,不必证明;
(2)类比探究:如图1,当点P在AB与CD之间时,猜想∠PFD与∠AEM的数量关系,并说明理由;
(3)拓展延伸:如图3,当点P在直线AB的上方时,PN交AB于点H,其他条件不变,猜想∠PFD与∠AEM的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+m的图象与反比例函数y= ![]() 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1). 
(1)求一次函数和反比例函数的解析式;
(2)求点C的坐标;
(3)结合图象直接写出不等式0<x+m≤ ![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段 BC上,联接AD交线段PQ于点E,且 ![]() =
= ![]() ,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.
,点G在BC延长线上,∠ACG的平分线交直线PQ于点F. 
(1)求证:PC=PE;
(2)当P是边AC的中点时,求证:四边形AECF是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王阿姨销售草莓,草莓成本价为每千克10元,她发现当销售单价为每千克至少10元,但不高于每千克20元时,销售量y(千克)与销售单价x(元)的函数图象如图所示: 
(1)求y关于x的函数解析式,并写出它的定义域;
(2)当王阿姨销售草莓获得的利润为800元时,求草莓销售的单价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com