
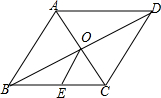
 如图,在菱形ABCD中,对角线AC与BD相交于点O,E为BC的中点,若BD=2$\sqrt{3}$cm,AC=2cm,则OE的长为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,E为BC的中点,若BD=2$\sqrt{3}$cm,AC=2cm,则OE的长为( )| A. | $\sqrt{3}$cm | B. | 2cm | C. | 1cm | D. | $\frac{\sqrt{3}}{2}$cm |
 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
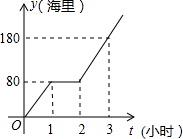 我国边防海警按照计划指定海域去巡逻,某巡逻艇匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达,如图是该艇行驶的路程y(海里)与所用时间t(小时)之间的函数图象,求该巡逻艇原计划准点到达指定海域所要行驶的路程.
我国边防海警按照计划指定海域去巡逻,某巡逻艇匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达,如图是该艇行驶的路程y(海里)与所用时间t(小时)之间的函数图象,求该巡逻艇原计划准点到达指定海域所要行驶的路程.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
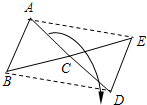 已知:如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180° 得到△DEC.
已知:如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180° 得到△DEC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
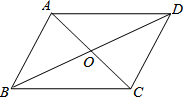 如图,平行四边形ABCD的对角线交于点O,且AB=4,△OCD的周长为20,则平行四边形ABCD的两条对角线的和是( )
如图,平行四边形ABCD的对角线交于点O,且AB=4,△OCD的周长为20,则平行四边形ABCD的两条对角线的和是( )| A. | 28 | B. | 32 | C. | 36 | D. | 46 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com