
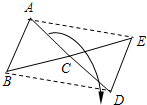
 已知:如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180° 得到△DEC.
已知:如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180° 得到△DEC.分析 (1)易证四边形ABDE是平行四边形,根据平行四边形的性质即可求解;
(2)根据平行四边形的性质:平行四边形的对角线互相平分,即可得到平行四边形的面积是△ABC的面积的四倍,据此即可求解;
(3)四边形ABDE是平行四边形,只要有条件:对角线相等即可得到四边形ABDE是矩形.
解答 解:(1)AE∥BD,且AE=BD;
(2)四边形ABDE的面积是:4×4=16;
(3)AC=BC.
理由是:∵AC=CD,BC=CE,
∴四边形ABDE是平行四边形.
∵AC=BC,
∴平行四边形ABDE是矩形.
点评 本题考查了图形的旋转以及平行四边形的判定与性质以及矩形的判定方法,正确理解四边形ABDE是平行四边形是关键.


科目:初中数学 来源: 题型:填空题
 某通讯公司推出了①②两种收费方式,收费y1,y2 (元)与通讯时间x(分钟)之间的函数关系如图所示,则使不等式kx+30<$\frac{1}{5}$x成立的x的取值范围是x>300.
某通讯公司推出了①②两种收费方式,收费y1,y2 (元)与通讯时间x(分钟)之间的函数关系如图所示,则使不等式kx+30<$\frac{1}{5}$x成立的x的取值范围是x>300.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
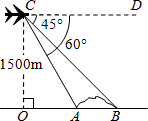 如图,在马航失联客机“MH370”搜寻中需要确定疑似海面上油污带AB的长度.已知在离地面1500m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求油污带AB的长.(参考数据:$\sqrt{3}$=1.73)
如图,在马航失联客机“MH370”搜寻中需要确定疑似海面上油污带AB的长度.已知在离地面1500m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求油污带AB的长.(参考数据:$\sqrt{3}$=1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
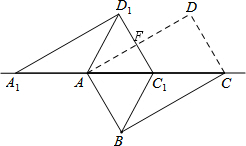 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1、BC1.
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1、BC1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 通过计算几何图形的面积可表示一些代数恒等式,右图可表示的代数恒等式是( )
通过计算几何图形的面积可表示一些代数恒等式,右图可表示的代数恒等式是( )| A. | (a-b)2=a2-2ab+b2 | B. | 2a(a+b)=2a2+2ab | C. | (a+b)2=a2+2ab+b2 | D. | (a+b)(a-b)=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
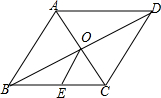 如图,在菱形ABCD中,对角线AC与BD相交于点O,E为BC的中点,若BD=2$\sqrt{3}$cm,AC=2cm,则OE的长为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,E为BC的中点,若BD=2$\sqrt{3}$cm,AC=2cm,则OE的长为( )| A. | $\sqrt{3}$cm | B. | 2cm | C. | 1cm | D. | $\frac{\sqrt{3}}{2}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
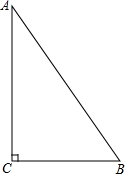 (1)如图,试用直尺与圆规在平面内确定一点O,使得点O到Rt△ABC的两边AC、BC的距离相等,并且点O到A、B两点的距离也相等.(不写作法,但需保留作图痕迹)
(1)如图,试用直尺与圆规在平面内确定一点O,使得点O到Rt△ABC的两边AC、BC的距离相等,并且点O到A、B两点的距离也相等.(不写作法,但需保留作图痕迹)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com