Question

【题目】如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD于点Q，PQ=3，PE=1．
（1）求证：AD=BE；
（2）求AD的长．

Answer 1

【答案】
（1）证明：∵△ABC为等边三角形，

∴AB=CA=BC，∠BAE=∠ACD=60°；

在△ABE和△CAD中，

，

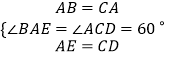∴△ABE≌△CAD（SAS），

∴AD=BE

（2）解：∵△ABE≌△CAD，

∴∠CAD=∠ABE，

∴∠BPQ=∠ABE+∠BAD=∠BAD+∠CAD=∠BAE=60°；

∵BQ⊥AD，

∴∠AQB=90°，

∴∠PBQ=90°﹣60°=30°，

∵PQ=3，

∴在Rt△BPQ中，BP=2PQ=6，

又∵PE=1，

∴AD=BE=BP+PE=6+1=7

【解析】（1）根据等边三角形的三条边都相等可得AB=CA，每一个角都是60°可得，∠BAE=∠ACD=60°，然后利用“边角边”证明△ABE和△CAD全等，根据全等三角形对应边相等证明即可；（2）根据全等三角形对应角相等可得∠CAD=∠ABE，然后求出∠BPQ=60°，再根据直角三角形两锐角互余求出∠PBQ=30°，然后根据直角三角形30°角所对的直角边等于斜边的一半求出BP=2PQ，再根据AD=BE=BP+PE代入数据进行计算即可得解．
【考点精析】认真审题，首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°)，还要掌握含30度角的直角三角形(在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半)的相关知识才是答题的关键．