
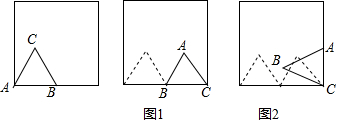
分析 先求出第一次到第六次旋转的路径的长分别是多少,探究规律后即可解决问题.
解答 解:第一次旋转的路径长为$\frac{120π•1}{180}$=$\frac{2}{3}$π,
第二次旋转的路径长为$\frac{30π•1}{180}$=$\frac{1}{6}$π,
第三次旋转的路径长为0,
第四次旋转的路径长为$\frac{1}{6}$π,
第五次旋转的路径长为$\frac{2}{3}$π,
第六次旋转的路径长为0,
…
由此发现每三次旋转的路径和为$\frac{2}{3}$π+$\frac{1}{6}$π=$\frac{5}{6}$π.
2016÷3=672,
∴完成第2016次无滑动滚动时,点A经过的路径总长为672×$\frac{5}{6}$π=560π.
故答案为560π
点评 本题考查旋转变换、等边三角形的性质、弧长公式等知识,解题的关键是学会从特殊到一般的探究方法,学会利用规律解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | a(1+m%)2 | B. | a(1+m%)3 | C. | a(1+m%)4 | D. | (a+m%)3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
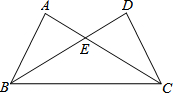 如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D=90°,AB=DC.
如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D=90°,AB=DC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
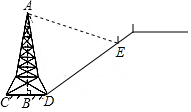 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=24 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为28.8m.
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=24 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为28.8m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com